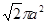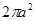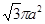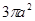题目内容
一个几何体的三视图如右图所示,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,则该几何体的外接球的表面积为 ( )
A. | B.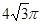 |
C. | D. |
C
解析试题分析:由三视图可知,原几何体为四棱锥,四棱锥的底面为边长是1的正方形,高为1,且一侧棱垂直底面,球心为最长侧棱的中点,所以外接球的半径为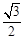 ,所以外接球的表面积为
,所以外接球的表面积为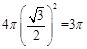 。
。
考点:三视图;球的表面积公式。
点评:做这类问题的关键是:根据三视图正确还原几何体的形状,并把外接球的球心位置找出。考查了学生的空间想象能力。属于常见题型。

练习册系列答案
相关题目
三棱锥 中,
中, 是底面,
是底面,

 且这四个顶点都在半径为2的球面上,
且这四个顶点都在半径为2的球面上, 则这个三棱锥的三个侧棱长的和的最大值为( )
则这个三棱锥的三个侧棱长的和的最大值为( )
| A.16 | B. | C. | D.32 |
网格纸的小正方形边长为1,一个正三棱锥的左视图如图所示,则这个正三棱锥的体积为( )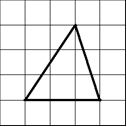
A.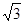 | B.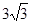 | C.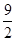 | D. |
如图是一个正三棱柱体的三视图,该柱体的体积等于
A. | B.2 | C.2 | D. |
如图,在正方体 中,点
中,点 在线段
在线段 上移动,则异面直线
上移动,则异面直线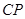 与
与 所成的角
所成的角 的取值范围( )
的取值范围( )
A. | B. |
C. | D. |

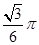
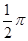
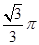
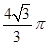



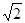
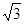
 为的正三棱锥
为的正三棱锥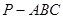 的侧面都是直角三角形,且四个顶点都在一个球面上,则球的表面积为( )
的侧面都是直角三角形,且四个顶点都在一个球面上,则球的表面积为( )