题目内容
已知球的直径SC=4,A,B是该球球面上的两点,AB=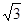 ,
,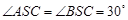 ,则棱锥S—ABC的体积为( )
,则棱锥S—ABC的体积为( )
A. | B.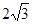 | C.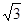 | D.1 |
C
解析试题分析:球心为点O,作AB中点D,连接OD,CD,说明SC是球的直径,利用余弦定理,三角形的面积公式求出S△SCD,和棱锥的高AB,即可求出棱锥的体积。
设球心为点O,作AB中点D,连接OD,CD 因为线段SC是球的直径,所以它也是大圆的直径,则易得:∠SAC=∠SBC=90°所以在Rt△SAC中,SC=4,∠ASC="30°" 得:AC=2,SA=2
又在Rt△SBC中,SC=4,∠BSC="30°" 得:BC=2,SB=2 则:SA=SB,AC=BC
则:SA=SB,AC=BC
因为点D是AB的中点所以在等腰三角形ASB中,SD⊥AB且SD=
在等腰三角形CAB中,CD⊥AB且CD=
又SD交CD于点D 所以:AB⊥平面SCD 即:棱锥S-ABC的体积:V= AB•S△SCD,
AB•S△SCD,
因为:SD= ,CD=
,CD= ,SC="4" 所以由余弦定理得:cos∠SDC=(SD2+CD2-SC2)
,SC="4" 所以由余弦定理得:cos∠SDC=(SD2+CD2-SC2)
则:sin∠SDC=
由三角形面积公式得△SCD的面积S= SD•CD•sin∠SDC="=3"
SD•CD•sin∠SDC="=3"
所以:棱锥S-ABC的体积:V= AB•S△SCD=
AB•S△SCD=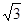 ,故选C
,故选C
考点:考查了简单几何体组合体的运用。
点评:本题是中档题,考查球的内接棱锥的体积的求法,考查空间想象能力,计算能力,有难度的题目,常考题型.

练习册系列答案
相关题目
半径为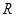 的半圆卷成一个圆锥,则它的体积为( ).
的半圆卷成一个圆锥,则它的体积为( ).
A.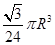 | B. | C. | D. |
网格纸的小正方形边长为1,一个正三棱锥的左视图如图所示,则这个正三棱锥的体积为( )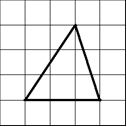
A.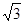 | B.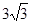 | C.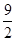 | D. |
若某多面体的三视图如图所示,则此多面体的体积是( )
| A.2 | B.4 | C.6 | D.12 |
如图,在正方体 中,点
中,点 在线段
在线段 上移动,则异面直线
上移动,则异面直线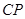 与
与 所成的角
所成的角 的取值范围( )
的取值范围( )
A. | B. |
C. | D. |
如果轴截面为正方形的圆柱的侧面积是4π,那么圆柱的体积等于( )
| A.π | B.2π | C.4π | D.8π |



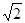
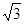
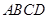 沿对角线
沿对角线 折成直二面角
折成直二面角 ,有如下四个结论:
,有如下四个结论: ⊥
⊥ 是等边三角形;③
是等边三角形;③ 与平面
与平面 所成的角为60°;④
所成的角为60°;④ 所成的角为60°.其中错误的结论是( )
所成的角为60°.其中错误的结论是( )