题目内容
已知一个空间几何体的三视图如图所示,则这个几何体的表面积是
A. | B. | C. | D. |
B
解析试题分析:根据题意可知该几何体是一个球体和一个半个圆柱体的组合体,球体的半径为1,而圆柱体的半径为1高为2,那么可知其表面积为 ,故选B.
,故选B.
考点:三视图的运用
点评:解决的关键是对于三视图还原为几何体结合几何体的表面积公式求解,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
一个几何体的三视图形状都相同,大小均相等,那么这个几何体不可以是( )
| A.球 | B.三棱锥 | C.正方体 | D.圆柱 |
三棱锥 中,
中, 是底面,
是底面,

 且这四个顶点都在半径为2的球面上,
且这四个顶点都在半径为2的球面上, 则这个三棱锥的三个侧棱长的和的最大值为( )
则这个三棱锥的三个侧棱长的和的最大值为( )
| A.16 | B. | C. | D.32 |
在一个几何体的三视图中,正视图和俯视图如下图所示,则该几何体的体积为( ) 
A. cm3( cm3( | B. cm3 cm3 | C. cm3 cm3 | D. cm3 cm3 |
半径为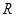 的半圆卷成一个圆锥,则它的体积为( ).
的半圆卷成一个圆锥,则它的体积为( ).
A.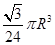 | B. | C. | D. |
已知结论:“在正三角形ABC中,若D是边BC的中点,G是三角形ABC的重心,则 ”。若把该结论推广到空间,则有结论:“在棱长都相等的四面体ABCD中,若
”。若把该结论推广到空间,则有结论:“在棱长都相等的四面体ABCD中,若 的中心为M,四面体内部一点O到四面体各面的距离都相等”,则
的中心为M,四面体内部一点O到四面体各面的距离都相等”,则 ( )
( )
| A.1 | B.2 | C.3 | D.4 |
从一个正方体中截去部分几何体,得到的几何体三视图如下,则此几何体的体积是( )
| A.64 | B. | C. | D. |
 的棱长为1,动点P在此正方体的表面上运动,且
的棱长为1,动点P在此正方体的表面上运动,且 ,记点P的轨迹的长度为
,记点P的轨迹的长度为 ,则函数的图像
,则函数的图像



