题目内容
【题目】求与圆（x﹣2）2+y2=2相切且在x轴，y轴上截距相等的直线方程．
【答案】解：若直线在x轴，y轴上截距相等， 则直线过原点，或直线斜率为﹣1，
当直线过原点时，设直线方程为：y=kx，即kx﹣y=0，
则由直线与圆（x﹣2）2+y2=2相切得： 
，
解得：k=±1，
即直线方程为：x﹣y=0，或x+y=0；
当直线斜率为1时，设直线方程为：x+y+C=0；
则由直线与圆（x﹣2）2+y2=2相切得： 
，
解得：C=0，或C=﹣4，
即直线方程为：x+y﹣4=0，或x+y=0；
综上可得直线方程为：x﹣y=0，x+y﹣4=0，或x+y=0
【解析】直线在x轴，y轴上截距相等，即直线过原点，或直线斜率为﹣1，进而得到答案．
【考点精析】掌握圆的标准方程是解答本题的根本，需要知道圆的标准方程：
；圆心为A(a,b),半径为r的圆的方程．
阅读快车系列答案
【题目】某研究机构对中学生记忆能力x和识图能力y进行统计分析，得到如下数据：
记忆能力x | 4 | 6 | 8 | 10 |
识图能力y | 3 | ﹡﹡﹡ | 6 | 8 |
由于某些原因，识图能力的一个数据丢失，但已知识图能力样本平均值是5.5．
（Ⅰ）求丢失的数据；
（Ⅱ）经过分析，知道记忆能力x和识图能力y之间具有线性相关关系，请用最小二乘法求出y关于x的线性回归方程 
；
（III）若某一学生记忆能力值为12，请你预测他的识图能力值．
【题目】下面给出了2010年亚洲一些国家的国民平均寿命（单位：岁）
国家 平均寿命 | 国家 平均寿命 | 国家 平均寿命 | 国家 平均寿命 | 国家 平均寿命 |
阿曼 76.1 | 泰国 73.7 | 阿富汗 59.0 | 尼泊尔 68.0 | 孟加拉国 70.1 |
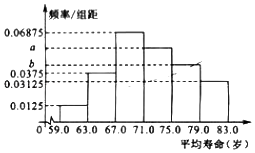
（1）请补齐频率分布表，并求出相应频率分布直方图中的a，b；
分组 | 频数 | 频率 |
[59.0，63.0） | 2 | 0.05 |
[63.0，67.0） | ||
[67.0，71.0） | ||
[71.0，75.0） | 9 | 0.225 |
[75.0，7.0） | 7 | 0.175 |
[79.0，83.0] | 5 | 0.125 |
合计 | 40 | 1.00 |
（2）请根据统计思想，利用(1)中的频率分布直方图估计亚洲人民的平均寿命． 