Question

【题目】若函数f（x）在定义域内存在实数x0 ， 使得f（x0+1）=f（x0）+f（1）成立，则称函数f（x）有“飘移点”x0 ． （Ⅰ）证明f（x）=x2+ex在区间 上有“飘移点”（e为自然对数的底数）；
（Ⅱ）若 在区间（0，+∞）上有“飘移点”，求实数a的取值范围．

Answer 1

【答案】（Ⅰ）证明：f（x）=x2+ex，设g（x）=f（x+1）f（x）f（1），

则g（x）=2x+（e1）exe．

因为g（0）=1， ，

所以 ．

所以g（x）=0在区间 上至少有一个实数根，

即函数f（x）=x2+ex在区间 上有“飘移点”．

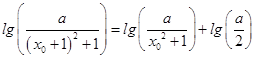（Ⅱ）解：函数 在区间（0，+∞）上有“飘移点”x0，即有 成立，即 ，

整理得 ．

从而问题转化为关于x的方程（2a）x22ax+22a=0在区间（0，+∞）上有实数根x0时实数a的范围．

设h（x）=（2a）x22ax+22a，由题设知a＞0．

当a＞2且x＞0时，h（x）＜0，方程h（x）=0无解，不符合要求；

当a=2时，方程h（x）=0的根为 ，不符合要求；

当0＜a＜2时，h（x）=（2a）x22ax+22a图象的对称轴是 ，

要使方程h（x）=0在区间（0，+∞）上有实数根，则只需△=4a24（2a）（22a）≥0，

解得 ．

所以 ，即实数a的取值范围是 ．

【解析】（Ⅰ）f（x）=x2+ex，设g（x）=f（x+1）f（x）f（1），则g（x）=2x+（e1）exe．只要判断g（0）g（ ）＜0即可．（II）函数 在区间（0，+∞）上有“飘移点”x0，即有 成立，即 ，整理得 ．从而问题转化为关于x的方程（2a）x22ax+22a=0在区间（0，+∞）上有实数根x0时实数a的范围．设h（x）=（2a）x22ax+22a，由题设知a＞0．对a分类讨论即可得出．