题目内容
【题目】如果实数x,y满足(x﹣2)2+y2=2,则 ![]() 的范围是( )
的范围是( )
A.(﹣1,1)
B.[﹣1,1]
C.(﹣∞,﹣1)∪(1,+∞)
D.(﹣∞,﹣1]∪[1,+∞)
【答案】B
【解析】解:设 ![]() =k,则y=kx表示经过原点的直线,k为直线的斜率.
=k,则y=kx表示经过原点的直线,k为直线的斜率.
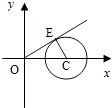
所以求 ![]() 的范围就等价于求同时经过原点和圆上的点的直线中斜率的范围.
的范围就等价于求同时经过原点和圆上的点的直线中斜率的范围.
从图中可知,斜率取最大值时对应的直线斜率为正且与圆相切,
此时的斜率就是其倾斜角∠EOC的正切值.
易得|OC|=2,|CE|= ![]() ,可由勾股定理求得|OE|=
,可由勾股定理求得|OE|= ![]() ,
,
于是可得到k=1,即为 ![]() 的最大值.
的最大值.
同理, ![]() 的最小值为﹣1,
的最小值为﹣1,
故选B.
【考点精析】本题主要考查了直线与圆的三种位置关系的相关知识点,需要掌握直线与圆有三种位置关系:无公共点为相离;有两个公共点为相交,这条直线叫做圆的割线;圆与直线有唯一公共点为相切,这条直线叫做圆的切线,这个唯一的公共点叫做切点才能正确解答此题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目