题目内容
18.下列有关命题的说法中,正确的是( )| A. | ?x∈R,lgx>0 | |
| B. | ?x0∈R,使得3${\;}^{{x}_{0}}$≤0 | |
| C. | “x=$\frac{π}{6}$”是“cosx=$\frac{\sqrt{3}}{2}$”的必要不充分条件 | |
| D. | “x=1”是“x≥1”的充分不必要条件 |
分析 根据对数函数和指数函数的性质判断A,B,根据充分不必要条件判断C,D,问题得以解决.
解答 解:对于选项A,?x∈R,lgx>0,因为对数函数的定义域为(0,+∞),故选项A错误,
对于选项B,?x0∈R,使得3${\;}^{{x}_{0}}$≤0,根据指数函数的性质,得到3x>0,故选项B错误,
对于选项C.“x=$\frac{π}{6}$”是“cosx=$\frac{\sqrt{3}}{2}$”的充分不必要条件,故选项C错误,
对于选项D,“x=1”是“x≥1”的充分不必要条件,因为“x=1”能推出x≥1,但是x≥1,不能推出x=1,故D正确.
故选:D
点评 本题考查了指数函数和对数函数性质,以及命题的逻辑关系,属于基础题.

练习册系列答案
相关题目
6.一个几何体的三视图如图,则其表面积为( )
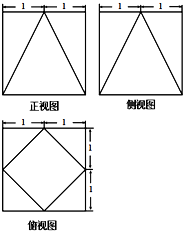

| A. | 20 | B. | 18 | C. | 14+2$\sqrt{3}$ | D. | 14+2$\sqrt{2}$ |
10.在五张卡片上分别写出有2,3,4,5,6这5个数字,其中6可以当9使用,从中任取3张,组成三位数,这样的三位数个数为( )
| A. | 60个 | B. | 70个 | C. | 96个 | D. | 136个 |
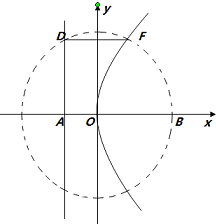 如图,抛物线E:y2=2px(p>0)的焦点为F,其准线l与x轴交于点A,过抛物线E上的动点p作PD⊥l于点D.当∠DPF=$\frac{2π}{3}$时,|PF|=4.
如图,抛物线E:y2=2px(p>0)的焦点为F,其准线l与x轴交于点A,过抛物线E上的动点p作PD⊥l于点D.当∠DPF=$\frac{2π}{3}$时,|PF|=4.