题目内容
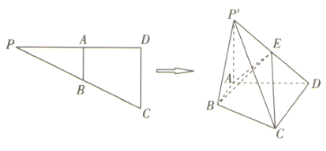
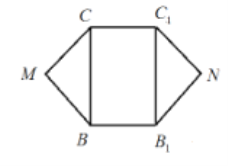
【题目】平面凸六边形![]() 的边长相等,其中
的边长相等,其中![]() 为矩形,
为矩形,![]() .将
.将![]() ,
,![]() 分别沿
分别沿![]() ,
,![]() 折至
折至![]() ,
,![]() ,且均在同侧与平面
,且均在同侧与平面![]() 垂直,连接
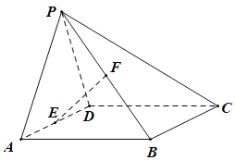
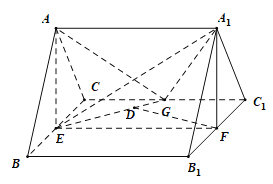
垂直,连接![]() ,如图所示,E,G分别是
,如图所示,E,G分别是![]() ,
,![]() 的中点.
的中点.
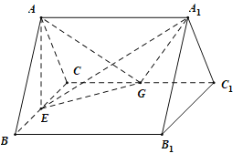
(1)求证:多面体![]() 为直三棱柱;
为直三棱柱;
(2)求二面角![]() 平面角的余弦值.
平面角的余弦值.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1) 取![]() 中点F,连接
中点F,连接![]() ,
,![]() ,再证明四边形
,再证明四边形![]() 为平行四边形,进而根据平行四边形的性质证得平面
为平行四边形,进而根据平行四边形的性质证得平面![]() 平面
平面![]() ,同时证得侧棱
,同时证得侧棱![]() 且互相相等,再证明
且互相相等,再证明![]() 平面
平面![]() 即可.
即可.
(2) 过F作![]() 交
交![]() 于点D,连接
于点D,连接![]() ,根据线面垂直的性质可得
,根据线面垂直的性质可得![]() 为二面角
为二面角![]() 的平面角以及二面角
的平面角以及二面角![]() 的平面角为
的平面角为![]() ,进而根据三角形中的边长关系结合勾股定理求解即可.
,进而根据三角形中的边长关系结合勾股定理求解即可.
(1)证明:取![]() 中点F,连接
中点F,连接![]() ,
,![]() .
.
∵F为![]() 中点,
中点,![]() ,又面
,又面![]() 平面
平面![]() ,
,
且面![]() 平面
平面![]() ,
,![]()
∴![]() 平面
平面![]() .
.

同理可证![]() 平面
平面![]() ,
,![]() ,而
,而![]() ,故四边形
,故四边形![]() 为平行四边形,从而
为平行四边形,从而![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,![]() ,故
,故![]() 且
且![]() ,因此四边形
,因此四边形![]() 为平面四边形,则
为平面四边形,则![]() ,
,
而![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,故
,故![]() 平面
平面![]() ;
;
由题设显然有![]() 平面
平面![]() ,而
,而![]() ,故平面
,故平面![]() 平面
平面![]() ,
,
又四边形![]() ,
,![]() 为平行四边形,则
为平行四边形,则![]() ,从而四边形
,从而四边形![]() 为平行四边形,而
为平行四边形,而![]() 平面
平面![]() ,因此多面体
,因此多面体![]() 为直三棱柱;
为直三棱柱;
(2)过F作![]() 交
交![]() 于点D,连接
于点D,连接![]() .
.
由(1)![]() 平面
平面![]() 知
知![]() ,而
,而![]() ,
,![]() ,因此
,因此![]() 平面
平面![]() ,则
,则![]() ,
,
故![]() 为二面角
为二面角![]() 的平面角,
的平面角,
而![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,则平面
,则平面![]() 平面
平面![]() ,
,
因此二面角![]() 的平面角为
的平面角为![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
从而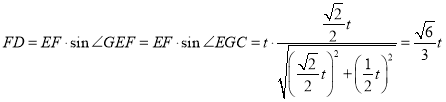 ,
,
故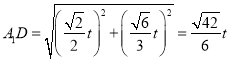 ,
,
则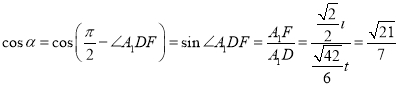

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目