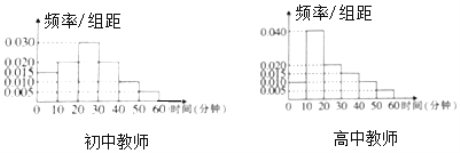
题目内容
【题目】如图,在四棱锥P—ABCD中,底面ABCD为矩形,平面PAD⊥平面ABCD,PAPD,E,F分别为AD,PB的中点.求证:
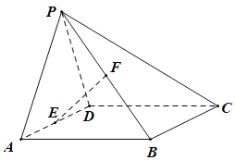
(1)EF//平面PCD;
(2)平面PAB平面PCD.
【答案】(1)见解析;(2)见解析
【解析】
(1)取BC中点G,连结EG,FG,推导出![]() ,
,![]() ,从而平面
,从而平面![]() 平面
平面![]() ,由此能得出结论;
,由此能得出结论;
(2)推导出![]() ,从而
,从而![]() 平面PAD,即得
平面PAD,即得![]() ,结合
,结合![]() 得出
得出![]() 平面PCD,由此能证明结论成立.
平面PCD,由此能证明结论成立.
(1)取BC中点G,连结EG,FG,∵E,F分别是AD,PB的中点,
∴![]() ,
,![]() ,
,
∴![]() 面
面![]() ,
,![]() 面
面![]() ,
,
∵![]() ,∴平面
,∴平面![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.

(2)因为底面ABCD为矩形,所以![]() ,
,
又因为平面![]() 平面ABCD,
平面ABCD,
平面![]() 平面
平面![]() ,
,![]() 平面ABCD,所以
平面ABCD,所以![]() 平面PAD.
平面PAD.
因为![]() 平面PAD,所以
平面PAD,所以![]() .
.
又因为![]() ,
,![]() ,所以
,所以![]() 平面PCD.
平面PCD.
因为![]() 平面PAB,所以平面
平面PAB,所以平面![]() 平面PCD.
平面PCD.

练习册系列答案
相关题目