题目内容
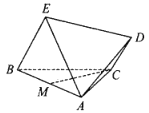
【题目】已知长方形ABCD中,AB=1,∠ABD=60°,现将长方形ABCD沿着对角线BD折起,使平面ABD⊥平面BCD,则折后几何图形的外接球表面积为_____.
【答案】4π
【解析】
设出球心的位置,利用勾股定理列方程组,解方程组求得球的半径,进而求得球的表面积.
长方形ABCD中,AB=1,∠ABD=60°,可得BD=2,AD![]() ,
,
作AE⊥BD于E,可得AEBD=ABAD,所以AE![]() ,BE
,BE![]() ,
,
因为平面ABD⊥平面BCD,AE![]() 面ABD,平面ABD∩平面BCD=BD,所以AE⊥面BCD,
面ABD,平面ABD∩平面BCD=BD,所以AE⊥面BCD,
由直角三角形BCD可得其外接圆的圆心为斜边BD的中点O1,且外接圆的半径r![]() 1,过O1作OO1垂直于底面BCD,所以EO1=O1B﹣BE=1
1,过O1作OO1垂直于底面BCD,所以EO1=O1B﹣BE=1![]() ,
,
所以OO1∥AE,取三棱锥外接球的球心O,设外接球的半径为R,
作OF⊥AE于F,则四边形EFOO1为矩形,O1E=OF,EF=OO1,则OA=OC=OB=OD=R,
在△AFO中,OA2=AF2+OF2=(AE﹣EF)2+EO12即R2=(![]() OO1)2
OO1)2![]() ;①
;①
在△BOO1中:OB2=OO12+EO12,即R2=OO12![]() ;②
;②
由①②可得R2=1,OO1=0,即外接球的球心为O1,所以外接球的表面积S=4πR2=4π,
故答案为:4π


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案【题目】党的十九大明确把精准脱贫作为决胜全面建成小康社会必须打好的三大攻坚战之一,为坚决打赢脱贫攻坚战,某帮扶单位考察了甲乙两种不同的农产品加工生产方式,现对两种生产方式加工的产品质量进行测试并打分对比,得到如下数据:
生产方式甲 | 分值区间 |
|
|
|
|
|
频数 | 20 | 30 | 100 | 40 | 10 | |
生产方式乙 | 分值区间 |
|
|
|
|
|
频数 | 25 | 35 | 60 | 50 | 30 |
其中产品质量按测试指标可划分为:指标在区间![]() 上的为特优品,指标在区间
上的为特优品,指标在区间![]() 上的为一等品,指标在区间
上的为一等品,指标在区间![]() 上的为二等品.
上的为二等品.
(1)用事件![]() 表示“按照生产方式甲生产的产品为特优品”,估计
表示“按照生产方式甲生产的产品为特优品”,估计![]() 的概率;
的概率;
(2)填写下面列联表,并根据列联表判断能否有![]() 的把握认为“特优品”与生产方式有关?
的把握认为“特优品”与生产方式有关?
特优品 | 非特优品 | |
生产方式甲 | ||
生产方式乙 |
(3)根据打分结果对甲乙两种生产方式进行优劣比较.
附表:
| 0.10 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
参考公式: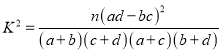 ,其中
,其中![]() .
.