题目内容
【题目】某中学举行的“新冠肺炎”防控知识闭卷考试比赛，总分获得一等奖、二等奖、三等奖的代表队人数情况如下表，该校政教处为使颁奖仪式有序进行，气氛活跃，在颁奖过程中穿插抽奖活动，并用分层抽样的方法从三个代表队中共抽取16人在前排就坐，其中一等奖代表队有6人.
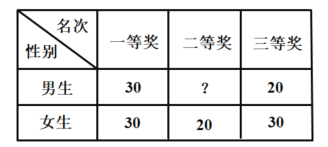
（1）求二等奖代表队的男生人数；
（2）从前排就坐的三等奖代表队员5人（2男3女）中随机抽取3人上台领奖，请求出只有一个男生上台领奖的概率；
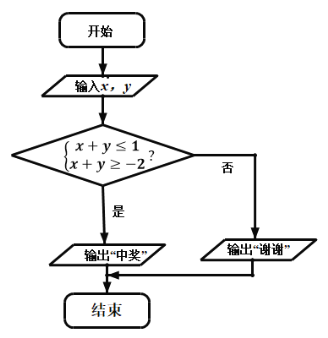
（3）抽奖活动中，代表队员通过操作按键，使电脑自动产生[
2，2]内的两个均匀随机数x，y，随后电脑自动运行如图所示的程序框图的相应程序，若电脑显示“中奖”，则代表队员获相应奖品；若电脑显示“谢谢”，则不中奖，求代表队队员获得奖品的概率.
【答案】（1）30；（2）
；（3）
.
【解析】
（1）先设季军队的男运动员人数为n，由分层抽样的方法得关于n的等式，即可解得n；
（2）设男生为A1，A2，女生为B1，B2，B3，随机抽取3人，利用列举法写出所有基本事件和只有一个男生上台领奖基本事件，最后利用概率公式即可计算得解；
（3）由框图得到，点（x，y）满足条件
，其表示的区域是图中阴影部分，利用几何概型的计算公式即可得到代表队队员获得奖品的概率.
（1）设代表队共有n人，则
，
所以n＝160，则三等奖代表队的男生人数为160
（30+30+20+20+30）＝30，
故所求二等奖代表队的男生人数为30人.
（2）设男生为A1，A2，女生为B1，B2，B3，随机抽取3人，包括的基本事件为A1A2B1，A1A2B2，A1A2B3，A1B1B2，
A1B1B3，A1B2B3，A2B1B2，A2B1B3，A2B2B3，B1B2B3，个数为10个，
只有一个男生上台领奖基本事件为A1B1B2，A1B1B3，A1B2B3，A2B1B2，A2B1B3，A2B2B3，个数为6个，
所以只有一个男生上台领奖的概率为
.
（3）试验的全部结果所构成的区域为Ω＝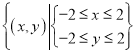
，
面积为SΩ＝4×4＝16，
事件A表示代表队队员获得奖品，所构成的区域为A＝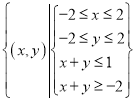
，
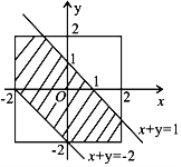
如图阴影部分的面积为：SA＝4
，
这是一个几何概型，所以P（A）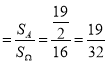
.
即代表队队员获得奖品的概率为.
【点晴】
本小题主要考查古典概型及其概率计算公式、程序框图、几何概型等基础知识，考查运算求解能力，属于中档题.
