题目内容
【题目】已知各项为正的数列
满足： 
， 
（
）.
（1）求
；
（2）证明： 
（
）；
（3）记数列
的前
项和为
，求证：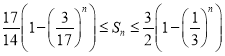 
.
【答案】(1) 
；(2)证明见解析；(3)证明见解析.
【解析】分析：（1）根据条件递推公式： 
， 
，依次推导
。（2）要证明
，故应由条件得到
，所以将条件
两边减去2得
，将右边通分，进而化为
由条件
，可得
。所以
与
异号。得到结论。（3）由（2）知
与
异号，要求数列
的前
项和为
，故应找数列
的间隔项的关系。由（2）知
，利用此关系式将式子中的
化成 
，并化简可得
（
）。
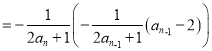
要找数列
的间隔项的关系，再变为
（
）。应判断式子右边的范围。由
可得 
（
）。进而得左边的范围
（
）。所以
与
同号。先求数列
前两项的范围， 
。进而可得数列
奇数项、偶数项的正负。即当
时， 
；当
时， 
。再分奇偶判断数列
奇数、偶数项的范围及单调性。可得
，结合条件可得
。由（2）知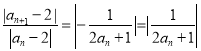
，故先求右边的范围
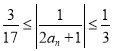，进而得
。利用累乘法可得
。再用等比数列求和公式可得
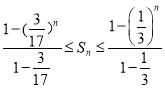。化简可得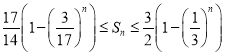
。
详解：（1）
（2）
与
异号
（3）由（2）知
（
）
（
）
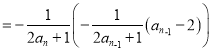所以
（
）
（
）
（
）
与
同号
又
当
时， 
当
时， 
①当
且
为偶数时
数列
递增且各项都小于2
②当
且
为奇数时
数列
递减且各项都大于2
由①②知， 
由（2）知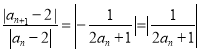
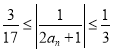
又
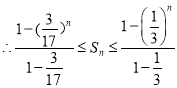
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
