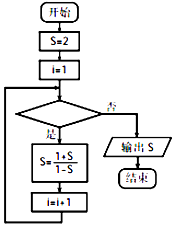
题目内容
【题目】已知函数f(x)=|2x﹣a|+|2x+3|,g(x)=|x﹣1|+2.
(Ⅰ)若a=1,解不等式f(x)<6;
(Ⅱ)若对任意x1∈R,都有x2∈R,使得f(x1)=g(x2)成立,求实数a的取值范围.
【答案】解:(Ⅰ)当a=1时,f(x)<6,即|2x﹣1|+|2x+3|<6,
即 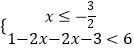 或
或 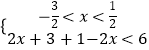 或
或 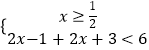 ,
,
∴ ![]() 或
或 ![]() 或
或 ![]() ,
,
∴﹣2<x<1,
所以不等式f(x)<6的解集为{x|﹣2<x<1}.
(Ⅱ)对任意x1∈R,都有x2∈R,使得f(x1)=g(x2)成立,
则有{y|y=f(x)}{y|y=g(x)},
又f(x)=|2x﹣a|+|2x+3|≥|(2x﹣a)﹣(2x+3)|=|a+3|,
g(x)=|x﹣1|+2≥2,从而|a+3|≥2,
解得a≤﹣5或a≥﹣1,
故a∈(﹣∞,﹣5]∪[﹣1,+∞)
【解析】(Ⅰ)通过讨论x的范围,得到关于x的不等式组,解出即可;(Ⅱ)问题转化为{y|y=f(x)}{y|y=g(x)},分别求出f(x),g(x)的最小值,得到关于a的不等式,解出即可.

 名校课堂系列答案
名校课堂系列答案【题目】调查表明:甲种农作物的长势与海拔高度、土壤酸碱度、空气湿度的指标有极强的相关性,现将这三项的指标分别记为x,y,z,并对它们进行量化:0表示不合格,1表示临界合格,2表示合格,再用综合指标ω=x+y+z的值评定这种农作物的长势等级,若ω≥4,则长势为一级;若2≤ω≤3,则长势为二级;若0≤ω≤1,则长势为三级,为了了解目前这种农作物长势情况,研究人员随机抽取10块种植地,得到如表中结果:
种植地编号 | A1 | A2 | A3 | A4 | A5 |
(x,y,z) | (1,1,2) | (2,1,1) | (2,2,2) | (0,0,1) | (1,2,1) |
种植地编号 | A6 | A7 | A8 | A9 | A10 |
(x,y,z) | (1,1,2) | (1,1,1) | (1,2,2) | (1,2,1) | (1,1,1) |
(Ⅰ)在这10块该农作物的种植地中任取两块地,求这两块地的空气湿度的指标z相同的概率;
(Ⅱ)从长势等级是一级的种植地中任取一块地,其综合指标为A,从长势等级不是一级的种植地中任取一块地,其综合指标为B,记随机变量X=A﹣B,求X的分布列及其数学期望.
【题目】随着人口老龄化的到来,我国的劳动力人口在不断减少,”延迟退休“已经成为人们越来越关注的话题,为了解公众对“延迟退休”的态度,某校课外研究性学习小组在某社区随机抽取了50人进行调查,将调查情况进行整理后制成下表:
年龄 | [20,25) | [25,30) | [30,35) | [35,40) | [40,45) |
人数 | 4 | 5 | 8 | 5 | 3 |
年龄 | [45,50) | [50,55) | [55,60) | [60,65) | [65,70) |
人数 | 6 | 7 | 3 | 5 | 4 |
经调查年龄在[25,30),[55,60)的被调查者中赞成人数分别是3人和2人,现从这两组的被调查者中各随机选取2人,进行跟踪调查.
(Ⅰ)求年龄在[25,30)的被调查者中选取的2人都赞成“延迟退休”的概率;
(Ⅱ)若选中的4人中,不赞成“延迟退休”的人数为X,求随机变量X的分布列和数学期望.