题目内容
在等差数列
中，若
，则有等式
成立，类比上述性质，在等比数列
中，若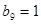
，则有等式 .
解析考点：类比推理．
分析：根据等差数列与等比数列通项的性质，结合类比的规则，和类比积，加类比乘，由类比规律得出结论即可．
解：在等差数列{an}中，若a10=0，则有等式a1+a2+…+an=a1+a2+…+a19-n成立（n＜19，n∈N*）．，
故相应的在等比数列{bn}中，若b9=1，则有等式b1b2…bn=b1b2…b17-n（n＜17，n∈N*）
故答案为：b1b2…bn=b1b2…b17-n（n＜17，n∈N*）．
练习册系列答案
阅读快车系列答案
相关题目
，
_________.
，
，
，
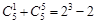
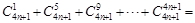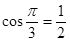中,归纳得出的一般结论（第n个等式）是___________。
是正实数，如果
，则有
，用类比思想推广，”设
是正实数，如果
，则 。
，
，
三种，其中
是正整数
的最佳分解时，我们规定函数
，例如
.关于函数
有下列叙述：①
，
，③
，④
.其中正确的序号为 （填入所有正确的序号）．
时，有
时，有
时，有
时，有
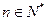时，你能得到的结论是： ．
，
，将M中的元素按从大到小顺序排列，则第2005个数是 .