题目内容
16.函数y=f(x)的最小正周期为2,且f(-x)=f(x).当x∈[0,1]时f(x)=-x+1,函数y=f(x)图象对称轴方程x=k(k∈Z),在区间[-3,4]上,函数G(x)=f(x)-($\frac{1}{2}$)|x|的零点个数有6个.分析 函数G(x)=f(x)-($\frac{1}{2}$)|x|的零点个数即为y=f(x)与y=($\frac{1}{2}$)|x|的图象的交点个数,只要由函数的性质,在同一个坐标系中作出两个函数的图象,即可的答案.
解答 解:由题意可知,函数G(x)=f(x)-($\frac{1}{2}$)|x|的零点个数即为y=f(x)与y=($\frac{1}{2}$)|x|的图象的交点个数,
函数y=f(x)周期为2,且为偶函数,函数y=($\frac{1}{2}$)|x|为偶函数,
在同一个坐标系中作出它们的图象,
可得对称轴方程为x=k(k∈Z),交点个数为6,
故答案是:x=k(k∈Z);6.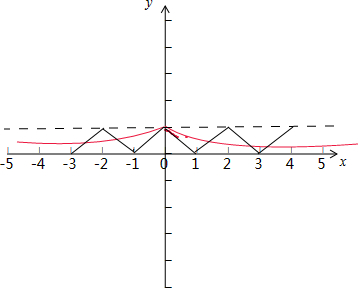
点评 本题考查由函数的性质作函数的图象,以及函数的零点问题转化成两函数图象的交点问题,同时考查了作图的能力,属中档题.

练习册系列答案
相关题目
6.下列说法:
①在残差图中,残差点比较均匀地落在水平的带状区域内,说明选用的模型比较合适;
②用相关指数可以刻画回归的效果,R2值越小说明模型的拟合效果越好;
③比较两个模型的拟合效果,可以比较残差平方和的大小,残差平方和越小的模型拟合效果越好.
其中说法正确的是( )
①在残差图中,残差点比较均匀地落在水平的带状区域内,说明选用的模型比较合适;
②用相关指数可以刻画回归的效果,R2值越小说明模型的拟合效果越好;
③比较两个模型的拟合效果,可以比较残差平方和的大小,残差平方和越小的模型拟合效果越好.
其中说法正确的是( )
| A. | ①② | B. | ②③ | C. | ①③ | D. | ①②③ |
7.在等比数列{an}中,a1=3,an>0,S3=21,则a3+a4+a5=( )
| A. | 84 | B. | 72 | C. | 33 | D. | 189 |
11.下列求导数运算错误的是( )
| A. | (3x)′=3xln3 | |
| B. | (x2lnx)′=2xlnx+x | |
| C. | $(\frac{cosx}{x})'=\frac{xsinx-cosx}{x^2}$ | |
| D. | $({2^{ln({x^2}+1)}})'=\frac{2xln2}{{{x^2}+1}}•{2^{ln({x^2}+1)}}$ |
8.如果复数z满足|z+3i|+|z-3i|=6,那么|z+1+i|的最小值是( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | $\sqrt{5}$ |