题目内容
已知数列 中,
中, ,
, ,对任意
,对任意 有
有 成立.
成立.
(I)若 是等比数列,求
是等比数列,求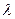 的值;
的值;
(II)求数列 的通项公式;
的通项公式;
(III)证明: 对任意
对任意 成立.
成立.
 中,
中, ,
, ,对任意
,对任意 有
有 成立.
成立.(I)若
 是等比数列,求
是等比数列,求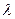 的值;
的值;(II)求数列
 的通项公式;
的通项公式;(III)证明:
 对任意
对任意 成立.
成立.解:(I)设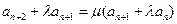 ,则
,则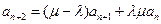 ,
,
令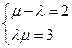 ,得
,得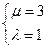 或者
或者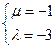 ,即
,即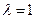 或
或 ;
;
(II)由(I)知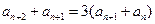 ,而
,而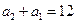 ,
,
故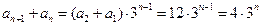 ,
,
同理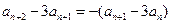 有
有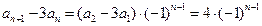 ,
,
两式作差得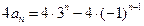 ,即
,即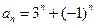 .
.
(III)当 时,注意到
时,注意到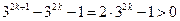 ,于是
,于是
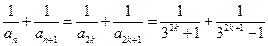
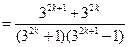
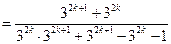
 .
.
显然当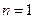 时,不等式成立;对于
时,不等式成立;对于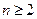 ,
,
当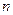 为奇数时,
为奇数时,
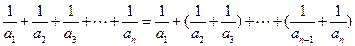
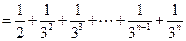
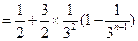
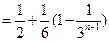
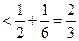 ;
;
当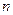 为偶数时,
为偶数时,
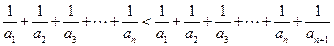
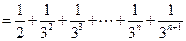
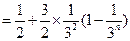
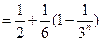
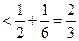 .
.
综上 对任意 有
有 成立.
成立.
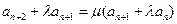 ,则
,则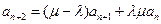 ,
,令
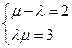 ,得
,得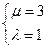 或者
或者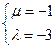 ,即
,即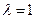 或
或 ;
;(II)由(I)知
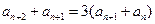 ,而
,而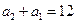 ,
,故
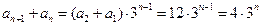 ,
,同理
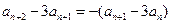 有
有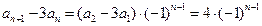 ,
,两式作差得
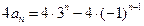 ,即
,即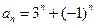 .
.(III)当
 时,注意到
时,注意到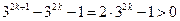 ,于是
,于是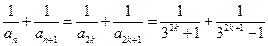
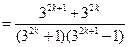
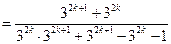
 .
.显然当
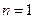 时,不等式成立;对于
时,不等式成立;对于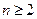 ,
,当
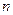 为奇数时,
为奇数时,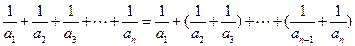
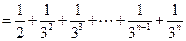
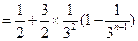
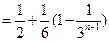
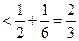 ;
;当
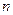 为偶数时,
为偶数时,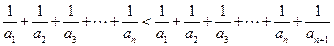
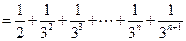
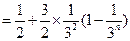
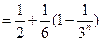
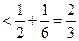 .
.综上 对任意
 有
有 成立.
成立.略

练习册系列答案
相关题目
 函数f(x)=
函数f(x)=  x
x  +
+  , h(x)=
, h(x)= 
 .
. ]=1og2 h(a-x)一log2h (4-x);
]=1og2 h(a-x)一log2h (4-x);  与
与 的大小.
的大小.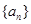 的前n项和为
的前n项和为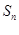 ,且
,且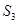 =6,
=6,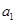 =4,则公差d等于
=4,则公差d等于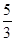
 2
2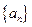 是公差不为零的等差数列,
是公差不为零的等差数列,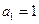 ,且
,且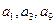 成等比数列.
成等比数列.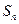 ;
;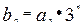 ,
, 求数列
求数列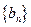 的前n项和
的前n项和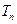
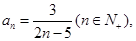 记数列
记数列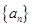 的前
的前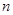 项和为
项和为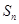 ,即
,即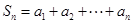 ,则使
,则使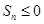 的
的 满足
满足 ( )
( )
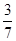


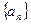 中,
中,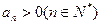 且
且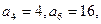 则数列
则数列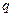 是 ( )
是 ( )
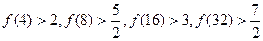 ,则推测当
,则推测当 时有
时有 