题目内容
(本题满分14分)已知顶点在原点, 焦点在x轴上的抛物线被直线y=2x+1截得的弦长为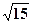 ,求抛物线的方程.
,求抛物线的方程.
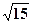 ,求抛物线的方程.
,求抛物线的方程.解:依题意可设抛物线方程为: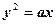 (a可正可负),与直线y=2x+1截得的弦为AB;
(a可正可负),与直线y=2x+1截得的弦为AB;
则可设A(x1,y1)、B(x2,y2)联立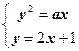 得
得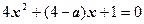
即: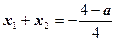
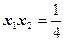 (6分)
(6分)
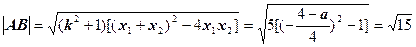
得:a=12或-4(6分)
所以抛物线方程为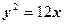 或
或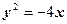 (2分)
(2分)
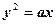 (a可正可负),与直线y=2x+1截得的弦为AB;
(a可正可负),与直线y=2x+1截得的弦为AB;则可设A(x1,y1)、B(x2,y2)联立
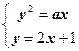 得
得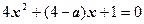
即:
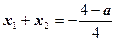
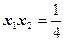 (6分)
(6分)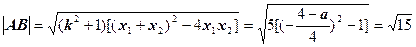
得:a=12或-4(6分)
所以抛物线方程为
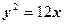 或
或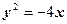 (2分)
(2分)略

练习册系列答案
相关题目
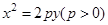 的焦点,另两个顶点在抛物线上,则满足此条件的正三角形共有
的焦点,另两个顶点在抛物线上,则满足此条件的正三角形共有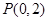 的直线
的直线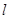 与抛物线
与抛物线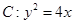 交于
交于 、
、 两点,
两点,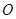 为坐标原点.
为坐标原点.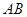 为直径的圆经过原点
为直径的圆经过原点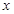 轴于点
轴于点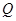 ,求
,求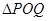 面积的取值范围.
面积的取值范围.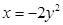 的准线方程是 ( )
的准线方程是 ( )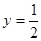
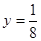
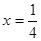
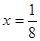
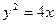 ,过点
,过点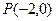 的直线AB交抛物线于点
的直线AB交抛物线于点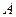 、
、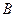 ,若线段
,若线段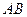 的垂直平分线交
的垂直平分线交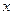 轴于点
轴于点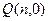 ,求
,求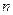 的取值范围.
的取值范围.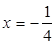 为准线的抛物线的标准方程为 ( )
为准线的抛物线的标准方程为 ( )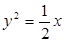
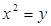
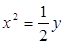
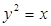
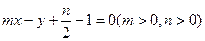 经过抛物线
经过抛物线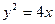 的焦点,则
的焦点,则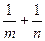 的
的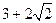
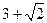
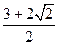
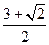
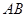 是过抛物线
是过抛物线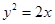 焦点的弦,
焦点的弦,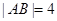 ,则
,则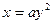 (a>0)的焦点,并且与x轴垂直,若l被抛物线截得的线段长为4,则a=
(a>0)的焦点,并且与x轴垂直,若l被抛物线截得的线段长为4,则a=