题目内容
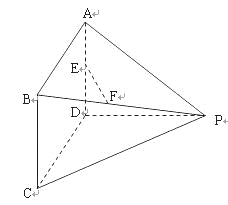
【题目】如图,在三棱柱![]() 中,每个侧面均为正方形,D为底边AB的中点,E为侧棱
中,每个侧面均为正方形,D为底边AB的中点,E为侧棱![]() 的中点.
的中点.

(1)求证:![]() 平面
平面![]() ;
;
(2)求证:![]() 平面
平面![]() ;
;
(3)若![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
【答案】(1)见解析
(2)见解析
(3)![]()
【解析】
(1)设![]() 和
和![]() 的交点为
的交点为![]() ,根据
,根据![]() ,且
,且![]() ,得到四边形
,得到四边形![]() 为平行四边形,故
为平行四边形,故![]() ,
,![]() 平面
平面![]() .
.
(2)证明![]() 平面
平面![]() ,可得
,可得![]() 平面
平面![]() ,故有
,故有![]() ,由正方形的两对角线的性质可得
,由正方形的两对角线的性质可得![]() ,
,
从而证得![]() 平面
平面![]() .
.
(3)利用等体积法将![]() 转化为求
转化为求![]() 可得.
可得.
证明:(1)设![]() 和
和![]() 的交点为O,连接EO,连接OD.
的交点为O,连接EO,连接OD.

因为O为![]() 的中点,D为AB的中点,
的中点,D为AB的中点,
所以![]() 且
且![]() .又E是
.又E是![]() 中点,
中点,
所以![]() ,且
,且![]() ,
,
所以![]() 且
且![]() .
.
所以,四边形ECOD为平行四边形.所以![]() .
.
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,则
,则![]() 平面
平面![]() .
.
(2)因为三棱柱各侧面都是正方形,所以![]() ,
,![]() .
.
所以![]() 平面ABC.因为
平面ABC.因为![]() 平面ABC,所以
平面ABC,所以![]() .
.
由已知得![]() ,所以
,所以![]() ,
,
所以![]() 平面
平面![]() .由(1)可知
.由(1)可知![]() ,所以
,所以![]() 平面
平面![]() .
.
所以![]() .因为侧面是正方形,所以
.因为侧面是正方形,所以![]() .
.
又![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(3)解:由条件求得![]() ,
,![]() ,可以求得
,可以求得![]()
所以![]()

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
【题目】在一块耕地上种植一种作物,每季种植成本为1000元,此作物的市场价格和这块地上的产量均具有随机性,且互不影响,其具体情况如下表:
作物产量( | 400 | 500 |
概率 |
|
|
作物市场价格(元/ | 5 | 6 |
概率 |
|
|
(1)设![]() 表示在这块地上种植1季此作物的利润,求
表示在这块地上种植1季此作物的利润,求![]() 的分布列(利润
的分布列(利润![]() 产量
产量![]() 市场价格
市场价格![]() 成本);
成本);
(2)若在这块地上连续3季种植此作物,求这3季中的利润都在区间![]() 的概率.
的概率.