题目内容
从集合{2,3,5,7,11,21,33,35,55}中任取三个数,则至少有两个数最大公约数大于1的概率是______.
从中任取三个数的事件总数为
=84种方法.
从中任取三个数,三个数的公约数为1的事件包括,
①从5个质数中任取三个数共
=10种方法;
②取一个或两个质数有如下取法(2、3、35),(2、3、55),(2、5、21),(2、5、33),(2、7、33),(2、7、55),(2、11、21),(2、11、35),(2、21、55),(2、33、35),(3、7、55),(3、11、35),(5、11、21),(5、7、33)共14种方法.
所以从中任取三个数,则至少有两个数最大公约数大于1的方法为84-10-14=60种方法.
所以从中任取三个数,则至少有两个数最大公约数大于1的概率是p=
=
.
故答案是
.
| C | 39 |
从中任取三个数,三个数的公约数为1的事件包括,
①从5个质数中任取三个数共
| C | 35 |
②取一个或两个质数有如下取法(2、3、35),(2、3、55),(2、5、21),(2、5、33),(2、7、33),(2、7、55),(2、11、21),(2、11、35),(2、21、55),(2、33、35),(3、7、55),(3、11、35),(5、11、21),(5、7、33)共14种方法.
所以从中任取三个数,则至少有两个数最大公约数大于1的方法为84-10-14=60种方法.
所以从中任取三个数,则至少有两个数最大公约数大于1的概率是p=
| 60 |
| 84 |
| 5 |
| 7 |
故答案是
| 5 |
| 7 |

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目

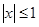 的概率为
的概率为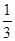 B
B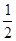 C
C D
D 