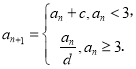题目内容
【题目】已知函数![]() ,且函数
,且函数![]() 为偶函数。
为偶函数。
(1)求![]() 的解析式;
的解析式;
(2)若方程![]() 有三个不同的实数根,求实数m的取值范围。
有三个不同的实数根,求实数m的取值范围。
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)利用![]() 是偶函数得到
是偶函数得到![]() 关于
关于![]() 对称,从而
对称,从而![]() ,解得a,进而得到解析式.
,解得a,进而得到解析式.
(2)问题转化为方程![]()
![]() 有三个不同实数根,令
有三个不同实数根,令![]() ,对
,对![]() 求导,研究单调性及极值,得到大致图像,由图可得m的范围.
求导,研究单调性及极值,得到大致图像,由图可得m的范围.
(1)由题可知![]() 所以函数
所以函数![]() 的对称轴为
的对称轴为![]() ,
,
由于![]() 是偶函数,
是偶函数,
所以![]() ,即
,即![]() 关于
关于![]() 对称
对称
所以![]() ,即
,即![]() ,
,
所以![]()
(2)方程![]() 有三个不同的实数根,即方程
有三个不同的实数根,即方程![]()
![]() 有三个不同实数根.
有三个不同实数根.
令![]() ,由(1)有
,由(1)有![]() ,
,
所以![]() ,令
,令![]() ,则
,则![]() 或
或![]() 。
。
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]()
故当![]() 时,
时,![]() 单调递增;当
单调递增;当![]() 时,
时,![]() 单调递减;当
单调递减;当![]() 时,
时,![]() 单调递增.
单调递增.
所以,当![]() 时,
时,![]() 取得极大值
取得极大值![]() ;当
;当![]() 时,
时,![]() 取得极小值,
取得极小值,![]()
又由于![]() ≥0,且当
≥0,且当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
其大致图像:
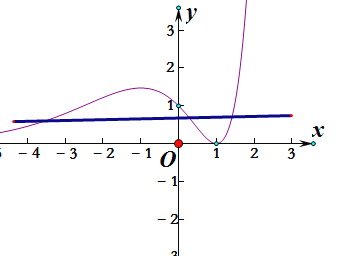
所以,方程![]()
![]() 有三个不同实数根时,m的范围是
有三个不同实数根时,m的范围是![]()

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
【题目】某学校共有教职工900人,分成三个批次进行继续教育培训,在三个批次中男、女教职工人数如下表所示.已知在全体教职工中随机抽取一名,抽到第二批次中女职工的概率是0.16.
第一批次 | 第二批次 | 第三批次 | |
女教职工 | 196 |
|
|
男教职工 | 204 | 156 |
|
(1)求![]() 的值;
的值;
(2)现用分层抽样的方法在全体教职工中抽取54名做培训效果的调查,问应在第三批次中抽取教职工多少名?
(3)已知![]() ,
,![]() ,求第三批次中女教职工比男教职工多的概率.
,求第三批次中女教职工比男教职工多的概率.