题目内容
.(本小题满分12分) 在公差不为零的等差数列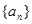 和等比数列
和等比数列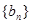 中,已知
中,已知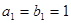 ,
,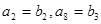 ;
;
(Ⅰ)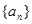 的公差
的公差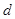 和
和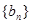 的公比
的公比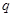 ;
;
(Ⅱ)设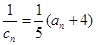 ,求数列
,求数列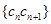 的前
的前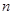 项和
项和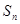
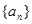 和等比数列
和等比数列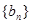 中,已知
中,已知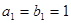 ,
,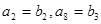 ;
; (Ⅰ)
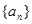 的公差
的公差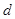 和
和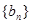 的公比
的公比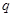 ;
;(Ⅱ)设
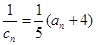 ,求数列
,求数列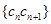 的前
的前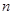 项和
项和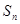
(Ⅰ)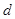 =5,
=5,
(Ⅱ)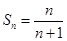
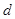 =5,
=5,
(Ⅱ)
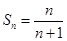
本试题主要是考查了等比数列和等差数列的通项公式和求和的综合运用。
(1)因为题意有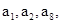 成等比,∴,即可以利用等比中项得到关系式
成等比,∴,即可以利用等比中项得到关系式
,从而的得到公差和公比的值。
(2)由(1)得: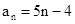 ,故可知
,故可知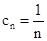 然后利用裂项相消的思想得到和式。
然后利用裂项相消的思想得到和式。
解:(Ⅰ)依题意有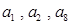 成等比,∴
成等比,∴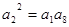 ,即
,即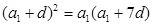
整理得 :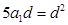 又∵
又∵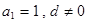 ,∴
,∴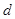 =5…………………………3分
=5…………………………3分
∴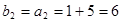 ,从而得
,从而得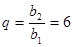 ……………………………………6分
……………………………………6分
(Ⅱ)由(1)得: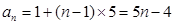 ,
,
∴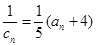 =n ∴
=n ∴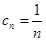 ,
, 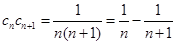 ……………9分
……………9分
∴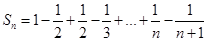
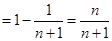 …………………………………12分
…………………………………12分
(1)因为题意有
 成等比,∴,即可以利用等比中项得到关系式
成等比,∴,即可以利用等比中项得到关系式,从而的得到公差和公比的值。
(2)由(1)得:
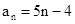 ,故可知
,故可知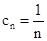 然后利用裂项相消的思想得到和式。
然后利用裂项相消的思想得到和式。解:(Ⅰ)依题意有
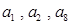 成等比,∴
成等比,∴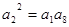 ,即
,即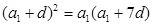
整理得 :
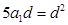 又∵
又∵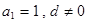 ,∴
,∴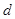 =5…………………………3分
=5…………………………3分∴
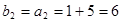 ,从而得
,从而得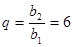 ……………………………………6分
……………………………………6分 (Ⅱ)由(1)得:
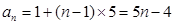 ,
,∴
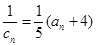 =n ∴
=n ∴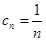 ,
, 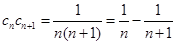 ……………9分
……………9分∴
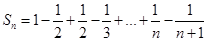
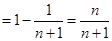 …………………………………12分
…………………………………12分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的首项
的首项 ,前
,前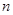 项和
项和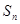 满足
满足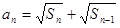
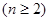 .
.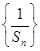 的前
的前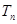 ,求证:
,求证: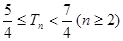 .
.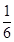 , 前n项和Sn=
, 前n项和Sn=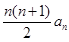 ,
,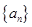 是公比大于1的等比数列,
是公比大于1的等比数列,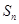 为数列
为数列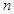 项和。已知
项和。已知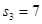 ,且
,且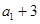 ,
,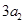 ,
,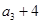 构成等差数列。
构成等差数列。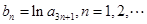 ,求数列
,求数列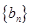 的前
的前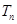 。
。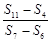 的值为 .
的值为 .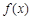 对任意
对任意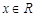 都有
都有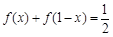 .
.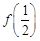 和
和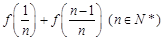 的值;
的值;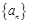 满足:
满足: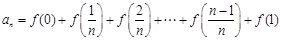 ,数列{an}是等差数列吗?请给予证明;
,数列{an}是等差数列吗?请给予证明;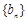 满足
满足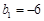 ,
,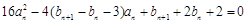 ,试求数列
,试求数列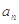 }中,各项都是正数,且
}中,各项都是正数,且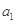 ,
,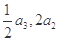 成等差数列,则
成等差数列,则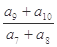 等于 ( )
等于 ( )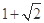
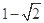
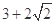
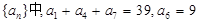 则数列
则数列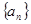 的前9项的和
的前9项的和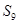 等于( )
等于( )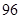 B
B 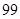 C
C 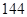 D 198
D 198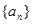 是非零等差数列,又
是非零等差数列,又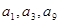 组成一个等比数列的前三项,
组成一个等比数列的前三项,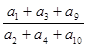 的值是 .
的值是 .