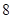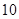题目内容
(12分)设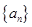 是公比大于1的等比数列,
是公比大于1的等比数列,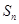 为数列
为数列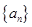 的前
的前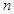 项和。已知
项和。已知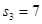 ,且
,且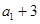 ,
,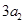 ,
,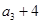 构成等差数列。
构成等差数列。
⑴求数列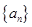 的通项;
的通项;
⑵令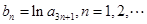 ,求数列
,求数列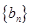 的前
的前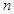 项和
项和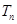 。
。
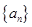 是公比大于1的等比数列,
是公比大于1的等比数列,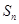 为数列
为数列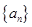 的前
的前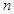 项和。已知
项和。已知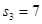 ,且
,且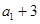 ,
,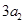 ,
,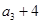 构成等差数列。
构成等差数列。⑴求数列
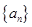 的通项;
的通项;⑵令
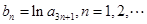 ,求数列
,求数列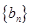 的前
的前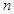 项和
项和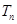 。
。⑴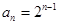 ⑵
⑵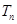
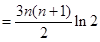
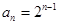 ⑵
⑵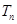
本试题主要是考查了数列的通项公式的 求解以及数列的求和的综合运用。
(1)由已知得: ,解得
,解得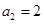 ,结合公比为q,得到关系式又
,结合公比为q,得到关系式又 可知
可知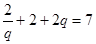 得到通项公式。
得到通项公式。
(2)由于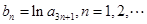 由⑴得
由⑴得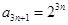
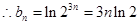
又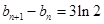
 是等差数列然后利用前n项和公式解得。
是等差数列然后利用前n项和公式解得。
解:⑴由已知得: ,解得
,解得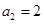 ……………………(2分)
……………………(2分)
设数列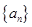 的公比为
的公比为 ,由
,由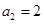 得
得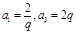 ,又
,又 可知
可知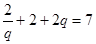 ,即
,即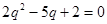 ,解得
,解得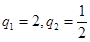 ………………………(4分)
………………………(4分)
由题意得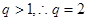 ,
,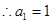 ……(5分)故数列
……(5分)故数列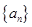 的通项公式为
的通项公式为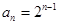 (6分)
(6分)
⑵由于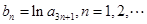 由⑴得
由⑴得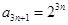
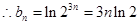 ……(8分)
……(8分)
又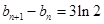
 是等差数列………………………(10分)
是等差数列………………………(10分)
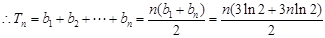
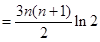 ……………(12分)
……………(12分)
(1)由已知得:
 ,解得
,解得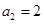 ,结合公比为q,得到关系式又
,结合公比为q,得到关系式又 可知
可知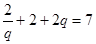 得到通项公式。
得到通项公式。(2)由于
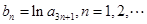 由⑴得
由⑴得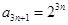
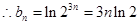
又
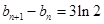
 是等差数列然后利用前n项和公式解得。
是等差数列然后利用前n项和公式解得。解:⑴由已知得:
 ,解得
,解得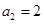 ……………………(2分)
……………………(2分)设数列
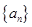 的公比为
的公比为 ,由
,由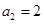 得
得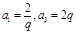 ,又
,又 可知
可知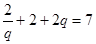 ,即
,即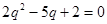 ,解得
,解得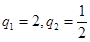 ………………………(4分)
………………………(4分)由题意得
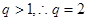 ,
,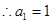 ……(5分)故数列
……(5分)故数列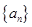 的通项公式为
的通项公式为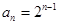 (6分)
(6分)⑵由于
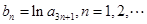 由⑴得
由⑴得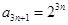
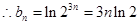 ……(8分)
……(8分)又
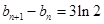
 是等差数列………………………(10分)
是等差数列………………………(10分)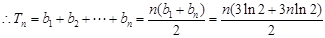
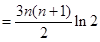 ……………(12分)
……………(12分)
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
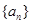 满足
满足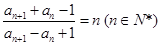 ,且
,且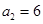 。
。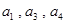 。
。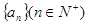 是等差数列,
是等差数列,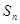 是其前
是其前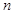 项和,
项和,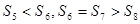 ,则下列结论错误的是( )
,则下列结论错误的是( )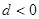
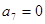
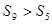
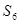 与
与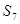 均为
均为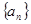 中,
中,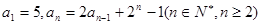 ,若存在实数
,若存在实数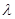 ,使得数列
,使得数列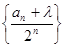 为等差数列,则
为等差数列,则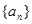 和等比数列
和等比数列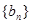 中,已知
中,已知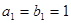 ,
,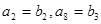 ;
; 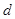 和
和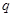 ;
;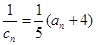 ,求数列
,求数列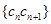 的前
的前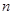 项和
项和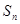
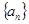 是等差数列,且
是等差数列,且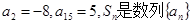 的前n项和,则 ( )
的前n项和,则 ( )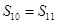 ;
;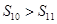 ;
; ;
;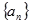 是公差不为零的等差数列,
是公差不为零的等差数列,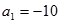 ,且
,且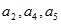 成等比数列.
成等比数列.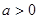 ,求数列
,求数列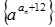 的前n项和
的前n项和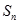 .
.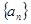 中,
中,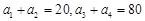 ,则
,则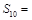 ________
________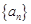 中,若
中,若 ,则
,则 ( )
( )