题目内容
(本题满分14分)数列{an}满足:a1=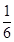 , 前n项和Sn=
, 前n项和Sn=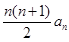 ,
,
(1)写出a2, a3, a4;(2)猜出an的表达式,并用数学归纳法证明.
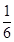 , 前n项和Sn=
, 前n项和Sn=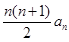 ,
,(1)写出a2, a3, a4;(2)猜出an的表达式,并用数学归纳法证明.
(1)a2=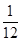 ;a3=
;a3=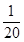 ;a4=
;a4=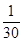
(2)an=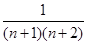
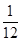 ;a3=
;a3=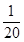 ;a4=
;a4=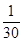
(2)an=
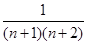
(1)根据an与Sn的关系,分别令n=2,3,4易求a2, a3, a4;
(2)根据前四项,可以猜想出an的表达式,由于问题是与正整数n有关,因而可以考虑采用数学归纳法进行证明.在用数学归纳法进行证明时,分两个步骤:一是验证n=1,等式成立;
二是先假设n=k时,等式成立;然后再证明n=k+1时,等式也成立,再证明时一定要用上n=k时的归纳假设,否则证明无效.
解:(1)令n="2," 得S2=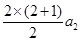 , 即a1+a2=3a2 , 解得a2=
, 即a1+a2=3a2 , 解得a2=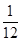 . ……………1分
. ……………1分
令n="3," 得S3=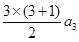 ,即a1+a2+a3=6a3, 解得a3=
,即a1+a2+a3=6a3, 解得a3=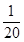 . ……………1分
. ……………1分
令n=4,得S4=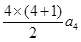 ,即a1+a2+a3+a4=10a4, 解得a4=
,即a1+a2+a3+a4=10a4, 解得a4=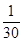 . ……………1分
. ……………1分
(2)由(1)的结果猜想an=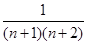 , 下面用数学归纳法给予证明:……………1分
, 下面用数学归纳法给予证明:……………1分
①当n=1时,a1=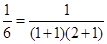 ,结论成立. ……………1分
,结论成立. ……………1分
②假设当n=k时,结论成立,即ak=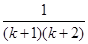 , ……………1分
, ……………1分
则当n=k+1时,Sk=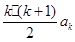 , (1) ……………1分
, (1) ……………1分
Sk+1=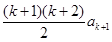 , (2) ……………1分
, (2) ……………1分
(2)-(1)得ak+1=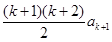 -
-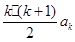 , ……………2分
, ……………2分
整理得ak+1=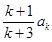 =
=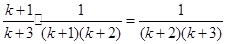 =
=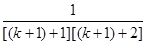 ,3分
,3分
即当n=k+1时结论也成立.
由①、②知对于n∈N+,上述结论都成立. ……………1分
(2)根据前四项,可以猜想出an的表达式,由于问题是与正整数n有关,因而可以考虑采用数学归纳法进行证明.在用数学归纳法进行证明时,分两个步骤:一是验证n=1,等式成立;
二是先假设n=k时,等式成立;然后再证明n=k+1时,等式也成立,再证明时一定要用上n=k时的归纳假设,否则证明无效.
解:(1)令n="2," 得S2=
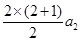 , 即a1+a2=3a2 , 解得a2=
, 即a1+a2=3a2 , 解得a2=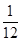 . ……………1分
. ……………1分令n="3," 得S3=
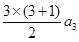 ,即a1+a2+a3=6a3, 解得a3=
,即a1+a2+a3=6a3, 解得a3=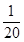 . ……………1分
. ……………1分令n=4,得S4=
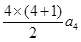 ,即a1+a2+a3+a4=10a4, 解得a4=
,即a1+a2+a3+a4=10a4, 解得a4=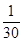 . ……………1分
. ……………1分(2)由(1)的结果猜想an=
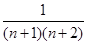 , 下面用数学归纳法给予证明:……………1分
, 下面用数学归纳法给予证明:……………1分①当n=1时,a1=
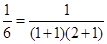 ,结论成立. ……………1分
,结论成立. ……………1分②假设当n=k时,结论成立,即ak=
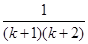 , ……………1分
, ……………1分则当n=k+1时,Sk=
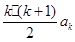 , (1) ……………1分
, (1) ……………1分Sk+1=
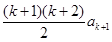 , (2) ……………1分
, (2) ……………1分(2)-(1)得ak+1=
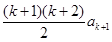 -
-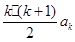 , ……………2分
, ……………2分整理得ak+1=
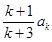 =
=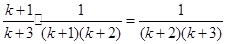 =
=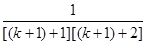 ,3分
,3分即当n=k+1时结论也成立.
由①、②知对于n∈N+,上述结论都成立. ……………1分

练习册系列答案
 同步奥数系列答案
同步奥数系列答案
相关题目
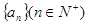 是等差数列,
是等差数列,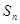 是其前
是其前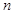 项和,
项和,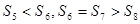 ,则下列结论错误的是( )
,则下列结论错误的是( )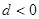
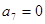
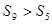
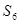 与
与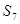 均为
均为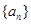 满足
满足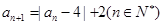 .
.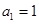 ,求
,求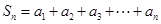 ;
;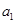 的值,使得数列
的值,使得数列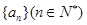 成等差数列.
成等差数列.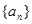 和等比数列
和等比数列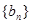 中,已知
中,已知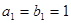 ,
,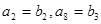 ;
; 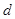 和
和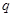 ;
;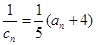 ,求数列
,求数列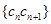 的前
的前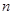 项和
项和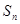
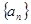 的前
的前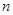 项和为
项和为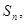 且
且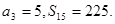
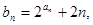 求数列
求数列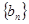 的前
的前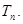
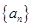 的前
的前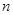 项和为
项和为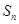 ,已知
,已知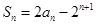 (n∈N*).
(n∈N*).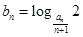 ,数列
,数列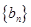 的前
的前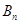 ,若存在整数
,若存在整数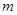 ,使对任意n∈N*且n ≥2,都有
,使对任意n∈N*且n ≥2,都有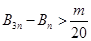 成立,求
成立,求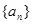 为等差数列,
为等差数列,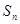 是其前n项和,且
是其前n项和,且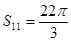 ,则
,则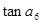 的值为( )
的值为( ) 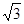
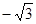

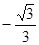
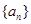 是首项为2,公差为1的等差数列,
是首项为2,公差为1的等差数列,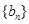 是首项为1,公比为2的等比数列,则数列
是首项为1,公比为2的等比数列,则数列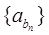 前10项的和等于 ( )
前10项的和等于 ( )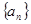 的前n项和,已知
的前n项和,已知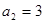 ,
,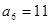 ,则
,则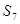 等于( )
等于( )