题目内容
(本小题满分14分)
已知正项数列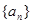 的首项
的首项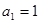 ,前
,前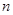 项和
项和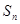 满足
满足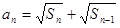
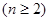 .
.
(Ⅰ)求数列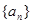 的通项公式;
的通项公式;
(Ⅱ)若数列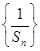 的前
的前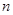 项和为
项和为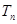 ,求证:
,求证: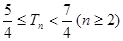 .
.
已知正项数列
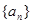 的首项
的首项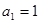 ,前
,前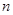 项和
项和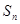 满足
满足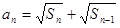
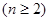 .
.(Ⅰ)求数列
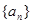 的通项公式;
的通项公式;(Ⅱ)若数列
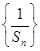 的前
的前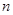 项和为
项和为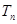 ,求证:
,求证: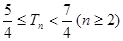 .
.(Ⅰ)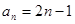 .(Ⅱ)证明:见解析。
.(Ⅱ)证明:见解析。
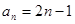 .(Ⅱ)证明:见解析。
.(Ⅱ)证明:见解析。本试题主要是考查了数列的 通项公式和数列求和的综合运用。
(1)因为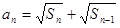 ,所以
,所以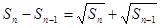 ,
,
即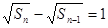 ,所以数列
,所以数列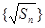 是首项为
是首项为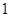 ,公差为
,公差为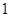 的等差数列,从而得到公式。
的等差数列,从而得到公式。
(2)证明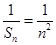 ,因为
,因为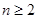 ,所以
,所以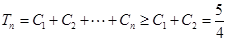 ,利用放缩法得到不等式的证明。
,利用放缩法得到不等式的证明。
(Ⅰ)解:因为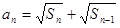 ,所以
,所以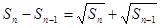 ,
,
即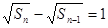 ,所以数列
,所以数列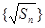 是首项为
是首项为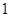 ,公差为
,公差为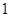 的等差数列,得
的等差数列,得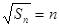 ,所以
,所以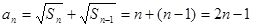
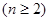 ,
,
当 时
时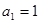 也适合. 所以
也适合. 所以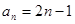 .…………………………………………7分
.…………………………………………7分
(Ⅱ)证明: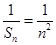 ,因为
,因为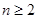 ,所以
,所以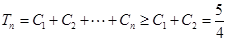 ;
;
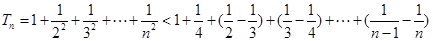
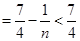 .
.
所以 ……………………………………………………………14分
……………………………………………………………14分
(1)因为
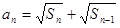 ,所以
,所以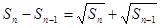 ,
,即
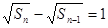 ,所以数列
,所以数列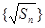 是首项为
是首项为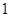 ,公差为
,公差为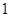 的等差数列,从而得到公式。
的等差数列,从而得到公式。(2)证明
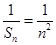 ,因为
,因为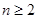 ,所以
,所以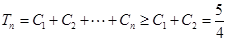 ,利用放缩法得到不等式的证明。
,利用放缩法得到不等式的证明。(Ⅰ)解:因为
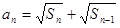 ,所以
,所以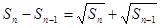 ,
,即
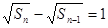 ,所以数列
,所以数列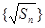 是首项为
是首项为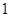 ,公差为
,公差为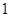 的等差数列,得
的等差数列,得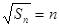 ,所以
,所以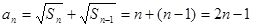
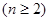 ,
,当
 时
时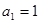 也适合. 所以
也适合. 所以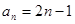 .…………………………………………7分
.…………………………………………7分(Ⅱ)证明:
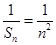 ,因为
,因为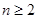 ,所以
,所以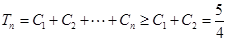 ;
;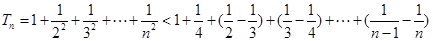
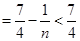 .
.所以
 ……………………………………………………………14分
……………………………………………………………14分
练习册系列答案
相关题目
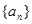 和等比数列
和等比数列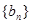 中,已知
中,已知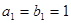 ,
,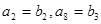 ;
; 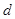 和
和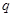 ;
;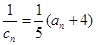 ,求数列
,求数列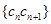 的前
的前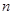 项和
项和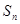
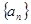 的前
的前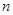 项和为
项和为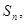 且
且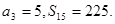
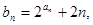 求数列
求数列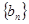 的前
的前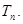
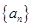 的前
的前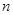 项和为
项和为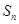 ,已知
,已知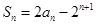 (n∈N*).
(n∈N*).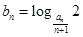 ,数列
,数列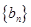 的前
的前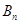 ,若存在整数
,若存在整数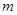 ,使对任意n∈N*且n ≥2,都有
,使对任意n∈N*且n ≥2,都有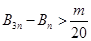 成立,求
成立,求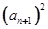 =
=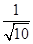
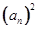 ,n
,n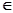 N*,
N*,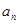 >0,令
>0,令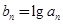 则数列
则数列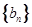 为( )
为( )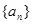 为等差数列,
为等差数列,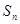 是其前n项和,且
是其前n项和,且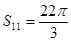 ,则
,则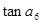 的值为( )
的值为( ) 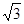
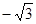

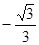
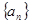 的前
的前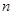 项和
项和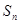 满足
满足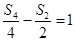 则数列
则数列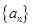 的前n项和为
的前n项和为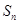 ,若
,若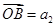
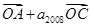 ,且A、B、C三点共线(O为该直线外一点),则
,且A、B、C三点共线(O为该直线外一点),则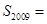 _________.
_________.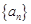 中,若
中,若 ,则
,则 ( )
( )