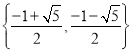题目内容
【题目】设![]() 是一个由
是一个由![]() 和
和![]() 构成的
构成的![]() 行
行![]() 列的数表,且
列的数表,且![]() 中所有数字之和不小于
中所有数字之和不小于![]() ,所有这样的数表构成的集合记为
,所有这样的数表构成的集合记为![]() ,记
,记![]() 为
为![]() 的第
的第![]() 行各数之和
行各数之和![]() ,
,![]() 为
为![]() 的第
的第![]() 列各数之和
列各数之和![]() ,
,![]() 为
为![]() 、
、![]() 、
、![]() ,
,![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 中的最大值.
中的最大值.
(1)对如下数表![]() ,求
,求![]() 的值;
的值;
|
|
|
|
|
|
|
|
(2)设数表![]() ,求
,求![]() 的最小值;
的最小值;
(3)已知![]() 为正整数,对于所有的
为正整数,对于所有的![]() ,
,![]() ,且
,且![]() 的任意两行中最多有
的任意两行中最多有![]() 列各数之和为
列各数之和为![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)计算出![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 的值,根据题中定义可得出
的值,根据题中定义可得出![]() 的值;
的值;
(2)由题意知,![]() 中所有数字之和的最小值为
中所有数字之和的最小值为![]() ,则
,则![]() 中至少有
中至少有![]() 个
个![]() ,只有当每行或每列都放
,只有当每行或每列都放![]() 个
个![]() ,才能使得
,才能使得![]() 取到最小值
取到最小值![]() ,然后就某行某列分别放
,然后就某行某列分别放![]() 个
个![]() 、
、![]() 个
个![]() 、
、![]() 个
个![]() ,列举出其他
,列举出其他![]() 行(或
行(或![]() 列)
列)![]() 的个数,得出
的个数,得出![]() 的最小值,于此得出
的最小值,于此得出![]() ;
;
(3)先计算出数表![]() 中的元素之和为
中的元素之和为![]() ,由题意定义得出
,由题意定义得出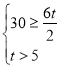 ,可得出
,可得出![]() ,然后分别就
,然后分别就![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 时就
时就![]() 的任意两行中数字之和为
的任意两行中数字之和为![]() 的列数进行分析,可得出
的列数进行分析,可得出![]() 的值.
的值.
(1)由题意可得![]() ,
,![]() ,
,
![]() ;
;
(2)由题意可得,![]() 中所有数字之和不小于
中所有数字之和不小于![]() ,即至少有
,即至少有![]() 个
个![]() .
.
而要使![]() 最小,则
最小,则![]() 中只有
中只有![]() 个
个![]() ,此时如表排列
,此时如表排列![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
下面利用来说明![]() .
.
①当某行某列全都是![]() 时,则其他
时,则其他![]() 行(或
行(或![]() 列)
列)![]() 的个数分别为:
的个数分别为:![]() 、
、![]() 、
、![]() 、
、![]() ,此时
,此时![]() ;
;
②当某行某列只放![]() 个
个![]() 时,则其他
时,则其他![]() 行(或
行(或![]() 列)
列)![]() 的个数分别为:
的个数分别为:![]() 、
、![]() 、
、![]() 、
、![]() ,则
,则![]() ;
;
③当某行过某列放![]() 个
个![]() 时,则其他
时,则其他![]() 行(或
行(或![]() 列)
列)![]() 的个数分别为:
的个数分别为:![]() 、
、![]() 、
、![]() 、
、![]() ,此时
,此时![]() .
.
由上可知,![]() ;
;
(3)![]() ,
,![]() 中所有数字之和为
中所有数字之和为![]() ,
,
由题意可得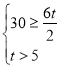 ,解得
,解得![]() .
.
①当![]() 时,每行中仅有
时,每行中仅有![]() 列为
列为![]() ,任意两行中至多有
,任意两行中至多有![]() 列和为
列和为![]() ,舍去;
,舍去;
②当![]() 时,每行中仅有
时,每行中仅有![]() 列为
列为![]() ,任意两行中至多有
,任意两行中至多有![]() 列和为
列和为![]() ,舍去;
,舍去;
③当![]() 时,如下表所示,每行中仅有
时,如下表所示,每行中仅有![]() 列为
列为![]() ,任意两行中至多有
,任意两行中至多有![]() 列和为
列和为![]() ,
,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
合乎题意;
④当![]() 或
或![]() 时,不成立.
时,不成立.
综上所述,![]() .
.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目