题目内容
【题目】(本小题满分14分)如图,三角形![]() 所在的平面与长方形
所在的平面与长方形![]() 所在的平面垂直,
所在的平面垂直,![]() ,
,![]() ,
,![]() .
.

(1)证明:![]() 平面
平面![]() ;
;
(2)证明:![]() ;
;
(3)求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
试题分析:(1)由四边形![]() 是长方形可证
是长方形可证![]() ,进而可证
,进而可证![]() 平面
平面![]() ;(2)先证
;(2)先证![]() ,再证
,再证![]() 平面
平面![]() ,进而可证
,进而可证![]() ;(3)取
;(3)取![]() 的中点
的中点![]() ,连结
,连结![]() 和
和![]() ,先证
,先证![]() 平面
平面![]() ,再设点
,再设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,利用
,利用![]() 可得
可得![]() 的值,进而可得点
的值,进而可得点![]() 到平面
到平面![]() 的距离.
的距离.
试题解析:(1)因为四边形![]() 是长方形,所以
是长方形,所以![]() ,因为
,因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]()
(2)因为四边形![]() 是长方形,所以
是长方形,所以![]() ,因为平面
,因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,因为
,因为![]() 平面
平面![]() ,所以
,所以![]()
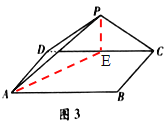
(3)取![]() 的中点
的中点![]() ,连结
,连结![]() 和
和![]() ,因为
,因为![]() ,所以
,所以![]() ,在
,在![]() 中,
中,![]()
![]() ,因为平面
,因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,由(2)知:
,由(2)知:![]() 平面
平面![]() ,由(1)知:
,由(1)知:![]() ,所以
,所以![]() 平面
平面![]() ,因为
,因为![]() 平面
平面![]() ,所以
,所以![]() ,设点
,设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,因为
,因为![]() ,所以
,所以![]() ,即
,即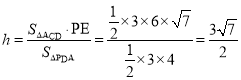 ,所以点
,所以点![]() 到平面
到平面![]() 的距离是
的距离是![]()

练习册系列答案
相关题目
【题目】设![]() 是一个由
是一个由![]() 和
和![]() 构成的
构成的![]() 行
行![]() 列的数表,且
列的数表,且![]() 中所有数字之和不小于
中所有数字之和不小于![]() ,所有这样的数表构成的集合记为
,所有这样的数表构成的集合记为![]() ,记
,记![]() 为
为![]() 的第
的第![]() 行各数之和
行各数之和![]() ,
,![]() 为
为![]() 的第
的第![]() 列各数之和
列各数之和![]() ,
,![]() 为
为![]() 、
、![]() 、
、![]() ,
,![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 中的最大值.
中的最大值.
(1)对如下数表![]() ,求
,求![]() 的值;
的值;
|
|
|
|
|
|
|
|
(2)设数表![]() ,求
,求![]() 的最小值;
的最小值;
(3)已知![]() 为正整数,对于所有的
为正整数,对于所有的![]() ,
,![]() ,且
,且![]() 的任意两行中最多有
的任意两行中最多有![]() 列各数之和为
列各数之和为![]() ,求
,求![]() 的值.
的值.