题目内容
已知函数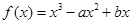 的图象为曲线E.
的图象为曲线E.
(1)若a = 3,b = -9,求函数f(x)的极值;
(2)若曲线E上存在点P,使曲线E在P点处的切线与x轴平行,求a,b的关系.
(1) ,
,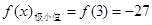 ;(2)
;(2)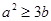 .
.
解析试题分析:(1)欲求函数极值应先求函数导数,并求出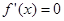 的根,再判断在根左右导数是否异号,若成立则此根为极值点,代入函数解析式可求极值.(2)对于存在性问题,一般假设存在然后依条件求出,若有则有,若无则假设不成立.
的根,再判断在根左右导数是否异号,若成立则此根为极值点,代入函数解析式可求极值.(2)对于存在性问题,一般假设存在然后依条件求出,若有则有,若无则假设不成立.
试题解析:
(1)当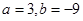 时,
时,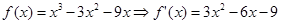 .令
.令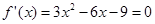 ,可得
,可得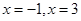 .
.区间 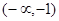
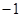
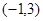
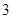
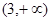
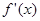
+ 0 - 0 + 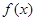
递增 极大值 递减 极小值 递增
当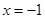 时,
时, ,当
,当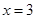 时,
时,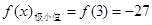 5分
5分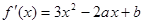 ,设切点为
,设切点为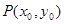 ,
,
则曲线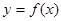 在点P的切线的斜率
在点P的切线的斜率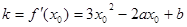
由题意知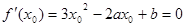 有解
有解
∴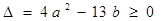 即
即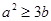 . 10分
. 10分
考点:(1)函数导数与极值;(2)函数导数与切线.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
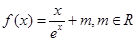 。
。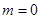 时,求
时,求 的单调区间、最大值;
的单调区间、最大值;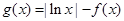 ,若存在实数
,若存在实数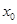 使得
使得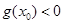 ,求m的取值范围。
,求m的取值范围。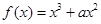 .
.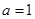 ,求函数
,求函数 的单调区间;
的单调区间;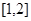 上是增函数,求
上是增函数,求 的取值范围.
的取值范围.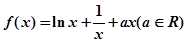
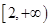 是单调减函数,求a的取值范围.
是单调减函数,求a的取值范围.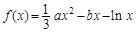 ,其中a,b∈R
,其中a,b∈R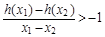 成立,试用a表示出b的取值范围.
成立,试用a表示出b的取值范围. (
(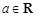 ).
).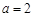 时,求
时,求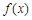 的图象在
的图象在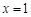 处的切线方程;
处的切线方程; 在
在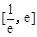 上有两个零点,求实数
上有两个零点,求实数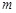 的取值范围;
的取值范围; 轴有两个不同的交点
轴有两个不同的交点 ,且
,且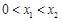 ,求证:
,求证: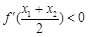 (其中
(其中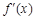 是
是 ex,a,b
ex,a,b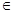 R,且a>0.
R,且a>0.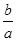 的取值范围.
的取值范围.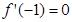 .
.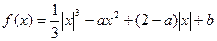 ,若
,若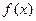 有六个不同的单调区间,
有六个不同的单调区间, 的取值范围为 ▲ .
的取值范围为 ▲ .