题目内容
已知函数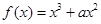 .
.
(1)若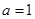 ,求函数
,求函数 的单调区间;
的单调区间;
(2)设函数 在区间
在区间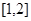 上是增函数,求
上是增函数,求 的取值范围.
的取值范围.
(1)递增区间是(?∞,?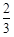 ),(0,+∞);递减区间是(?
),(0,+∞);递减区间是(?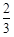 ,0).(2)[-
,0).(2)[-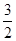 ,+
,+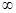 ).
).
解析试题分析:(1)求出 导函数,解出当
导函数,解出当 =1时,
=1时, >0对应的区间就是
>0对应的区间就是 的增区间,
的增区间, <0对应的区间就是
<0对应的区间就是 的减区间;(2)由函数
的减区间;(2)由函数 在区间
在区间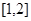 上是增函数知
上是增函数知 ≥0对
≥0对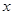 ∈[1,2]恒成立,通过参变分离化为a≥?
∈[1,2]恒成立,通过参变分离化为a≥?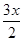 对
对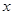 ∈[1,2]恒成立,求出?
∈[1,2]恒成立,求出?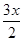 在
在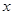 ∈[1,2]上的最大值,则a大于等于?
∈[1,2]上的最大值,则a大于等于?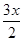 在
在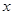 ∈[1,2]上的最大值,即得到a的取值范围.
∈[1,2]上的最大值,即得到a的取值范围.
试题解析: =
=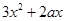 ,
,
(1)当a=1时, =
= ,
,
令 =0得x=0或x=?
=0得x=0或x=?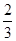
∴当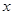 变化时,
变化时, ,
, 的变化情况如下表
的变化情况如下表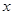
(?∞,? 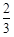 )
)? 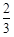
(? 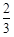 ,0)
,0)0 (0,+∞) 
+ 0 - 0 + 
↑ 极大值 ↓ 极小值 ↑
∴ 的递增区间是(?∞,?
的递增区间是(?∞,?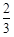 ),(0,+∞);递减区间是(?
),(0,+∞);递减区间是(?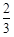 ,0).
,0).
(2)∵函数 在区间[1,2]上是增函数,
在区间[1,2]上是增函数,
∴对任意的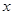 ∈[1,2]恒有
∈[1,2]恒有 ≥0,即对任意的
≥0,即对任意的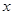 ∈[1,2]恒有a≥?
∈[1,2]恒有a≥?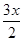
∴a≥[?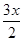 ]max,而函数y=?
]max,而函数y=?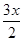 在区间[1,2]上是减函数,
在区间[1,2]上是减函数,
∴当
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
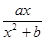 在x=1处取得极值2.
在x=1处取得极值2.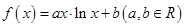 ,在点
,在点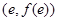 处的切线方程是
处的切线方程是 (e为自然对数的底)。
(e为自然对数的底)。 的值及
的值及 的解析式;
的解析式; 是正数,设
是正数,设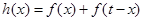 ,求
,求 的最小值;
的最小值;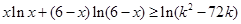 对一切
对一切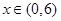 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。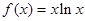 .
.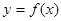 在点(1,0)处的切线方程;
在点(1,0)处的切线方程;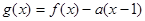 ,其中
,其中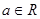 ,求函数
,求函数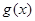 在
在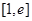 上的最小值.(其中
上的最小值.(其中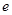 为自然对数的底数)
为自然对数的底数)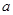 是实数,函数
是实数,函数 .
.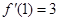 ,求
,求 在点
在点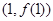 处的切线方程.
处的切线方程. 在
在 上的最大值.
上的最大值.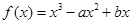 的图象为曲线E.
的图象为曲线E.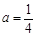 时,求函数y=f(x)的极值;
时,求函数y=f(x)的极值;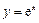 的图象在点
的图象在点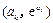 处的切线与
处的切线与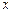 轴的交点的横坐标为
轴的交点的横坐标为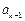 ,其中
,其中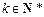 ,
,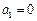 ,则
,则