题目内容
函数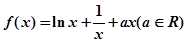
(1)a=0时,求f(x)最小值;
(2)若f(x)在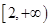 是单调减函数,求a的取值范围.
是单调减函数,求a的取值范围.
(1)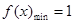 ;(2)
;(2)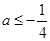
解析试题分析:(1)求函数最值问题,对于这类含有对数和分式的函数(只要是几种初等函数的四则复合)往往采用求导数的方法,利用函数的单调性求函数最值;(2)含参量函数性质讨论问题,往往都涉及导数.
试题解析:
(1)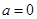 时
时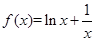 ,
,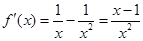 , 3分
, 3分 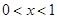 时
时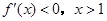 时
时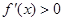 ,
,
∴f(x)在(0,1)单减,在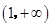 单增, 5分
单增, 5分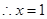 时
时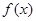 有最小值1 6分
有最小值1 6分
方法一: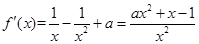 ,
,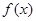 在
在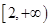 为减函数,则
为减函数,则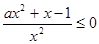 ,
,
即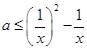 ,当
,当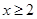 恒成立,∴
恒成立,∴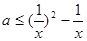 最小值 9分
最小值 9分
令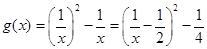 ,
,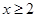 则
则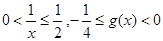 ,
,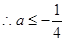 12分
12分
方法二:要使函数在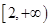 为减函数,
为减函数,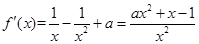 可知
可知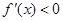 , 9分
, 9分
即在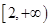 ,
,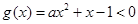 ,则有
,则有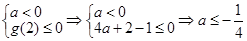 . 12分
. 12分
考点:(1)导数与函数单调性;(2)含参量恒成立问题(一般采用分离常数法),特殊函数性质讨论法.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
 ,函数
,函数 (
( 为自然对数的底数).
为自然对数的底数). ,求函数
,求函数 的单调区间;
的单调区间; ,求
,求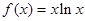 .
.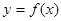 在点(1,0)处的切线方程;
在点(1,0)处的切线方程;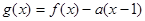 ,其中
,其中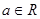 ,求函数
,求函数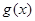 在
在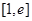 上的最小值.(其中
上的最小值.(其中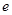 为自然对数的底数)
为自然对数的底数) ,其中
,其中 ,
, 为自然对数的底数.
为自然对数的底数. 是函数
是函数 的导函数,求函数
的导函数,求函数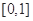 上的最小值;
上的最小值; ,函数
,函数 内有零点,求
内有零点,求 的取值范围。
的取值范围。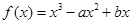 的图象为曲线E.
的图象为曲线E. (
(
 R).
R). 时,求函数
时,求函数 的极值;
的极值; 轴有且只有一个交点,求
轴有且只有一个交点,求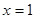 是函数
是函数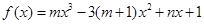 的一个极值点,其中
的一个极值点,其中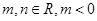 .
.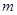 与
与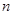 的关系式;
的关系式;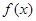 的单调区间;
的单调区间;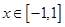 时,函数
时,函数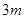 ,求
,求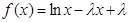 (
(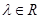 ).
). 的单调区间;
的单调区间;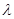 使
使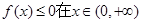 上恒成立?若存在,请求实数
上恒成立?若存在,请求实数 (x)在(a,b)
(x)在(a,b) 
 象如图示,则函数f(x)在(a,b)内极小值点的个数为___________
象如图示,则函数f(x)在(a,b)内极小值点的个数为___________