Question

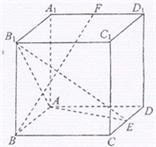如图，在正方体ABCD-A₁B₁C₁D₁中，E、F分别是CD、A₁D₁中点
（1）求证：AE⊥BF；
（2）求证：AB₁⊥BF；
（3）棱CC₁上是否存在点P，使BF⊥平面AEP，若存在，确定点P位置；若不存在，说明理由．

Answer 1

分析：（1）取AD中点G，连接FG、BG，通过证明FG⊥AE，AE⊥BG，BG∩FG=G，证明AE⊥平面BFG，说明AE⊥BF．
（2）连A₁B，证明AB₁⊥A₁B，AB₁⊥BF，AE∩AB₁=A，证明BF⊥平面AB₁E．（8分）
（3）存在，取CC₁中点P，连接EP、C₁D说明AP?平面AB₁E，由（2）知BF⊥平面AB₁E，推出AP⊥BF．
方法2：（1）建立空间直角坐标系如图，设正方体棱长为2a，证明

BF

•

AE

=-2a2+2a2+0=0，

BF

⊥

AE

，得到AE⊥BF．
（2）利用

BF

•

AB1

=0，

BF

⊥

AB1

，∴BF⊥AB₁，且AB₁∩AE=A，说明BF⊥平面AB₁E．
（3）设点P（2a，2a，z），0≤z≤2a，则

AP

=（2a，2a，z），若AP⊥BF，

BF

•

AP

=-4a2+2a2+2az=0，
求出z得到P（2a，2a，c），即点P在CC₁中点处．

解答：（1）证明：取AD中点G，连接FG、BG，
则FG⊥AE，
又∵△BAG≌△ADE，∴∠ABG=∠DAE，
∴AE⊥BG，又∵BG∩FG=G，
∴AE⊥平面BFG，
∴AE⊥BF．（8分）
（2）证明：连A₁B，则AB₁⊥A₁B，
又AB₁⊥A₁F，∴AB₁⊥平面A₁BF，
∴AB₁⊥BF，
又AE∩AB₁=A，
∴BF⊥平面AB₁E．（8分）
（3）存在，取CC₁中点P，即为所求，
连接EP、C₁D
∵EP∥C₁D，C₁D∥AB₁，
∴EP∥AB₁，∴AP?平面AB₁E，
由（2）知BF⊥平面AB₁E，∴AP⊥BF．（12分）
方法2：
（1）建立空间直角坐标系如图，设正方体棱长为2a，则
A（0，0，0），B（2a，0，0），B₁（2a，0，2a），E（a，2a，0），
F（0，a，2a），
∴

BF

=(-2a，a，2a)，

AB1

=(2a，0，2a)，

AE

=(a，2a，0)
∴

BF

•

AE

=-2a2+2a2+0=0，
∴

BF

⊥

AE

，∴AE⊥BF．（4分）
（2）∵

BF

•

AB1

=-4a²+0+4a²=0，
∴

BF

⊥

AB1

，∴BF⊥AB₁，且AB₁∩AE=A，
∴BF⊥平面AB₁E．（8分）
（3）设点P（2a，2a，z），0≤z≤2a，则

AP

=(2a，2a，z)，
若AP⊥BF，

BF

•

AP

=-4a2+2a2+2az=0，
∴z=a，∴P（2a，2a，c），即点P在CC₁中点处．（12分）

点评：本小题考查空间线面、线线垂直的判定及互相转化，考查数形结合、化归与转化的数学思想方法，以及空间想象能力、推理论证能力和运算求解能力．