题目内容
【题目】已知函数![]() .
.
(1)证明函数![]() 在
在![]() 上是减函数,
上是减函数,![]() 上是增函数;
上是增函数;
(2)若方程![]() 有且只有一个实数根,判断函数
有且只有一个实数根,判断函数![]() 的奇偶性;
的奇偶性;
(3)在(2)的条件下探求方程![]() 的根的个数.
的根的个数.
【答案】(1)证明详见解析;(2)![]() 为偶函数;(3)
为偶函数;(3)![]() 时
时![]() 只有一解,
只有一解,![]() 时
时![]() 有两解.
有两解.
【解析】
试题分析:(1)函数![]() ,利用函数单调性定义进行证明,设
,利用函数单调性定义进行证明,设![]() 的
的![]() 上任意两个不等的实数,且
上任意两个不等的实数,且![]() ,则
,则![]() ,
,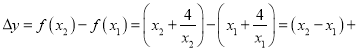
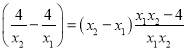 ,由于
,由于![]() ,所以
,所以![]() ,则
,则![]() ,所以函数
,所以函数![]() 在区间
在区间![]() 上单调递减,同理可证在区间
上单调递减,同理可证在区间![]() 单调递增;(2)方程
单调递增;(2)方程![]() 等价于方程
等价于方程![]() 有且只有一个实数根,则
有且只有一个实数根,则![]() ,因为
,因为![]() ,所以
,所以![]() ,则此时函数
,则此时函数![]() ,
,![]() ,易证明函数
,易证明函数![]() 为奇函数;(3)在(2)的条件下,
为奇函数;(3)在(2)的条件下,![]() 即
即![]() ,根据第(2)证明所得的单调性可知,当
,根据第(2)证明所得的单调性可知,当![]() 即
即![]() 时
时![]() 只有一解 ,当
只有一解 ,当![]() 即
即![]() 时
时![]() 有两解.
有两解.
试题解析:(1)由题意:![]() 任取
任取![]() 且使
且使![]()
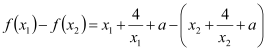
![]()
![]()
![]()
![]()
![]()
则![]()
![]() 在
在![]() 上是减函数
上是减函数
同理可证 ![]() 在
在 ![]() 上是增函数
上是增函数
(2)由题意知方程![]() 有且只有一个实数根
有且只有一个实数根
![]() 又
又![]()
![]()
此时![]() ,
,![]()
又![]() 的定义域为
的定义域为![]() 关于原点对称,
关于原点对称,
且![]() ,
,
![]() 是奇函数
是奇函数
(3)由(2)知![]() 可化为
可化为![]()
又由(1)(2)知:
当![]() 即
即![]() 时
时![]() 只有一解
只有一解
当![]() 即
即![]() 时
时![]() 有两解
有两解
综上,当![]() 时
时![]() 只有一解;
只有一解;
当![]() 时
时![]() 有两解;
有两解;

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某单位共有10名员工,他们某年的收入如下表:
员工编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
年薪(万元) | 3 | 3.5 | 4 | 5 | 5.5 | 6.5 | 7 | 7.5 | 8 | 50 |
(1)从该单位中任取2人,此2人中年薪收入高于5万的人数记为![]() ,求
,求![]() 的分布列和期望;
的分布列和期望;
(2)已知员工年薪收入![]() 与工作所限
与工作所限![]() 成正相关关系,某员工工作第一年至第四年的年薪如下表:
成正相关关系,某员工工作第一年至第四年的年薪如下表:
工作年限 | 1 | 2 | 3 | 4 |
年薪(万元) | 3.0 | 4.2 | 5.6 | 7.2 |
预测该员工第五年的年薪为多少?
附:线性回归方程![]() 中系数计算公式和参考数据分别为:
中系数计算公式和参考数据分别为:
 ,
,![]() ,其中
,其中![]() 为样本均值,
为样本均值,![]() ,
,![]() ,(
,(![]() )
)
