题目内容
(本小题满分14分)已知函数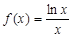 ,
,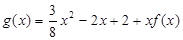 .
.
(Ⅰ)求函数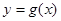 的单调区间;(Ⅱ)若函数
的单调区间;(Ⅱ)若函数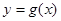 在[
在[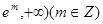 上有零点,求
上有零点,求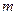 的最大值;(Ⅲ)证明:
的最大值;(Ⅲ)证明: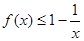 在其定义域内恒成立,并比较
在其定义域内恒成立,并比较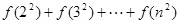 与
与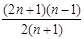 (
(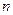
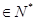 且
且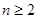 )的大小.
)的大小.
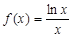 ,
,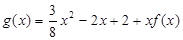 .
.(Ⅰ)求函数
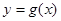 的单调区间;(Ⅱ)若函数
的单调区间;(Ⅱ)若函数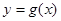 在[
在[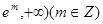 上有零点,求
上有零点,求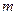 的最大值;(Ⅲ)证明:
的最大值;(Ⅲ)证明: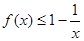 在其定义域内恒成立,并比较
在其定义域内恒成立,并比较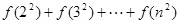 与
与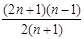 (
(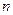
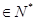 且
且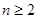 )的大小.
)的大小.(Ⅰ)单调递增区间为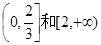 ,单调递减区间为
,单调递减区间为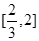 (Ⅱ) -2(Ⅲ)略
(Ⅱ) -2(Ⅲ)略
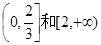 ,单调递减区间为
,单调递减区间为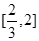 (Ⅱ) -2(Ⅲ)略
(Ⅱ) -2(Ⅲ)略:(Ⅰ)由题知: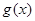 的定义域为(0,+∞)∵
的定义域为(0,+∞)∵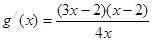
∴函数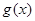 的单调递增区间为
的单调递增区间为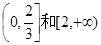
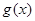 的单调递减区间为
的单调递减区间为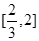
(Ⅱ)∵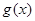 在x∈
在x∈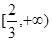 上的最小值为
上的最小值为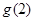
且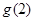 =
=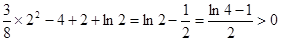
∴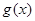 在x∈
在x∈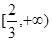 上没有零点,∴要想使函数
上没有零点,∴要想使函数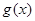 在
在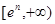 (n∈Z)上有零点,并考虑到
(n∈Z)上有零点,并考虑到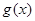 在
在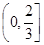 单调递增且在
单调递增且在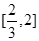 单调递减,故只须
单调递减,故只须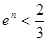 且
且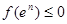 即可,
即可,
易验证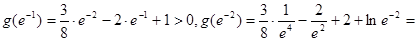
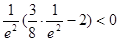 ,当n≤-2且n∈Z时均有
,当n≤-2且n∈Z时均有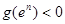 ,即函数
,即函数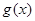 在
在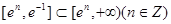 上有零点,∴n的最大值为-2.
上有零点,∴n的最大值为-2.
(Ⅲ)要证明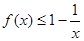 ,即证
,即证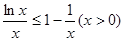 只须证lnx-x+1
只须证lnx-x+1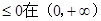 上恒成立.令h(x)=lnx-x+1(x>0),由
上恒成立.令h(x)=lnx-x+1(x>0),由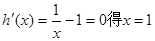
则在x=1处有极大值(也是最大值)h(1)=0∴lnx-x+1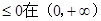 上恒成立.
上恒成立.
∴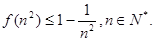 ∴
∴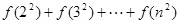
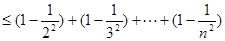
=(n-1)-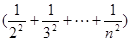 <(n-1)-[
<(n-1)-[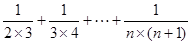 ]
]
=(n-1)-(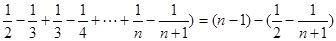
=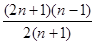 ∴
∴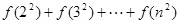 <
<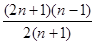 .
.
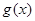 的定义域为(0,+∞)∵
的定义域为(0,+∞)∵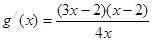
∴函数
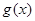 的单调递增区间为
的单调递增区间为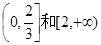
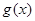 的单调递减区间为
的单调递减区间为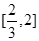
(Ⅱ)∵
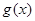 在x∈
在x∈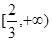 上的最小值为
上的最小值为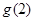
且
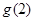 =
=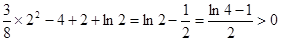
∴
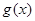 在x∈
在x∈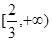 上没有零点,∴要想使函数
上没有零点,∴要想使函数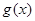 在
在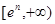 (n∈Z)上有零点,并考虑到
(n∈Z)上有零点,并考虑到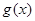 在
在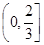 单调递增且在
单调递增且在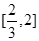 单调递减,故只须
单调递减,故只须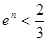 且
且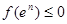 即可,
即可,易验证
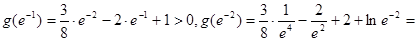
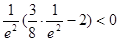 ,当n≤-2且n∈Z时均有
,当n≤-2且n∈Z时均有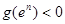 ,即函数
,即函数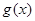 在
在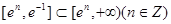 上有零点,∴n的最大值为-2.
上有零点,∴n的最大值为-2.(Ⅲ)要证明
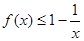 ,即证
,即证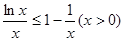 只须证lnx-x+1
只须证lnx-x+1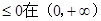 上恒成立.令h(x)=lnx-x+1(x>0),由
上恒成立.令h(x)=lnx-x+1(x>0),由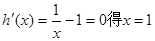
则在x=1处有极大值(也是最大值)h(1)=0∴lnx-x+1
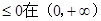 上恒成立.
上恒成立.∴
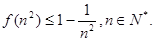 ∴
∴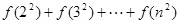
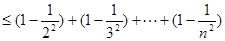
=(n-1)-
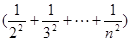 <(n-1)-[
<(n-1)-[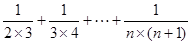 ]
]=(n-1)-(
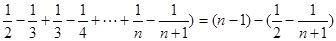
=
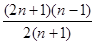 ∴
∴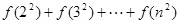 <
<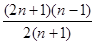 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
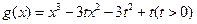
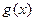 的单调区间;
的单调区间;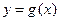 在点
在点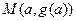 和
和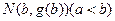 处的切线都与
处的切线都与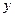 轴垂直,若方程
轴垂直,若方程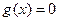 在区间
在区间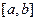 上有解,求实数
上有解,求实数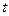 的取值范围。
的取值范围。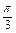 ;
;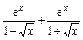 ,x0=2;
,x0=2;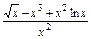 ,x0=1.
,x0=1.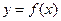 是定义域为R的偶函数,其图像均在x轴的上方,对任意的
是定义域为R的偶函数,其图像均在x轴的上方,对任意的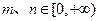 ,都有
,都有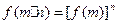 ,且
,且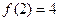 ,又当
,又当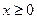 时,其导函数
时,其导函数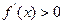 恒成立。
恒成立。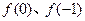 的值;
的值;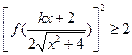 ,其中
,其中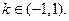
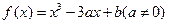 .(Ⅰ)若曲线
.(Ⅰ)若曲线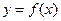 在点
在点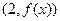 处与直线
处与直线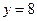 相切,求
相切,求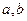 的值;(Ⅱ)求函数
的值;(Ⅱ)求函数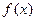 的单调区间与极值点.
的单调区间与极值点.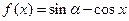 ,则
,则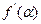 等于( )
等于( )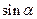



 ,
, =
= ,
, ,则
,则 是( )
是( )






