题目内容
设二次函数f(x)=ax2+bx+c(a≠0)满足条件:①当x∈R时,f(x-4)=f(2-x),且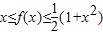 ;②f(x)在R上的最小值为0.
;②f(x)在R上的最小值为0.(1)求f(1)的值及f(x)的解析式;
(2)若g(x)=f(x)-k2x在[-1,1]上是单调函数,求k的取值范围;
(3)求最大值m(m>1),使得存在t∈R,只要x∈[1,m],就有f(x+t)≤x.
【答案】分析:(1)有条件得 ,求出f(1)=1,再由条件求出函数的对称轴,由函数的最小值列出方程求出a、b、c的值,代入解析式化简即可;
,求出f(1)=1,再由条件求出函数的对称轴,由函数的最小值列出方程求出a、b、c的值,代入解析式化简即可;
(2)由(1)求出g(x)化简后,求出函数的对称轴,再由二次函数的单调性和条件列出不等式,求出k的值;
(3)先假设存在,对f(x)配方后,再由分离常数法把条件转化为: ,判断出函
,判断出函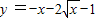 的单调性,求出最大值和最小值,结合t求出m的最大值.
的单调性,求出最大值和最小值,结合t求出m的最大值.
解答:解:(1)∵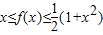 在R上恒成立,
在R上恒成立,
∴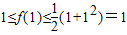 ,即f(1)=1
,即f(1)=1
∵f(x-4)=f(2-x),∴函数图象关于直线x=-1对称,
∴ .
.
∵f(1)=1,∴a+b+c=1
又∵f(x)在R上的最小值为0,
∴f(-1)=0,即a-b+c=0,
由 ,解得
,解得 ,
,
∴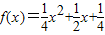 ;
;
(2)由(1)得, ,
,
∴g(x)对称轴方程为x=2k2-1,
∵g(x)在[-1,1]上是单调函数,
∴2k2-1≤-1或2k2-1≥1,
解得k≥1或k≤-1或k=0,
∴k的取值范围是k≥1或k≤-1或k=0.
(3)假设存在存在t∈R满足条件,
由(1)知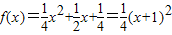 ,
,
∴f(x+t)≤x?(x+t+1)2≤4x且x∈[1,m],
?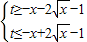 在[1,m]上恒成立?
在[1,m]上恒成立?
∵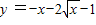 在[1,m]上递减,
在[1,m]上递减,
∴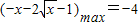 ,
,
∵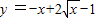 在[1,m]上递减,
在[1,m]上递减,
∴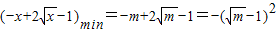
∴ ,∴
,∴ ,
,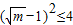 ,
,
∵m>1,∴ ,
,
∴m≤9,∴m的最大值为9.
点评:本题考查了二次函数的性质的综合应用,待定系数法求函数的解析式,以及分离常数法处理恒成立问题,第(3)问出现了两个未知数,注意结合点,考查了转化思想,难度较大.
 ,求出f(1)=1,再由条件求出函数的对称轴,由函数的最小值列出方程求出a、b、c的值,代入解析式化简即可;
,求出f(1)=1,再由条件求出函数的对称轴,由函数的最小值列出方程求出a、b、c的值,代入解析式化简即可;(2)由(1)求出g(x)化简后,求出函数的对称轴,再由二次函数的单调性和条件列出不等式,求出k的值;
(3)先假设存在,对f(x)配方后,再由分离常数法把条件转化为:
 ,判断出函
,判断出函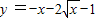 的单调性,求出最大值和最小值,结合t求出m的最大值.
的单调性,求出最大值和最小值,结合t求出m的最大值.解答:解:(1)∵
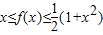 在R上恒成立,
在R上恒成立,∴
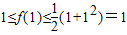 ,即f(1)=1
,即f(1)=1∵f(x-4)=f(2-x),∴函数图象关于直线x=-1对称,
∴
 .
.∵f(1)=1,∴a+b+c=1
又∵f(x)在R上的最小值为0,
∴f(-1)=0,即a-b+c=0,
由
 ,解得
,解得 ,
,∴
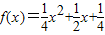 ;
;(2)由(1)得,
 ,
,∴g(x)对称轴方程为x=2k2-1,
∵g(x)在[-1,1]上是单调函数,
∴2k2-1≤-1或2k2-1≥1,
解得k≥1或k≤-1或k=0,
∴k的取值范围是k≥1或k≤-1或k=0.
(3)假设存在存在t∈R满足条件,
由(1)知
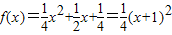 ,
,∴f(x+t)≤x?(x+t+1)2≤4x且x∈[1,m],
?
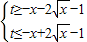 在[1,m]上恒成立?
在[1,m]上恒成立?
∵
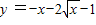 在[1,m]上递减,
在[1,m]上递减,∴
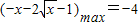 ,
,∵
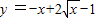 在[1,m]上递减,
在[1,m]上递减,∴
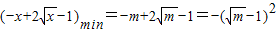
∴
 ,∴
,∴ ,
,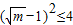 ,
,∵m>1,∴
 ,
,∴m≤9,∴m的最大值为9.
点评:本题考查了二次函数的性质的综合应用,待定系数法求函数的解析式,以及分离常数法处理恒成立问题,第(3)问出现了两个未知数,注意结合点,考查了转化思想,难度较大.

练习册系列答案
相关题目
设二次函数f(x)=ax2+bx+c(a>0),方程f(x)-x=0的两个根x1、x2满足0<x1<x2<
,且函数f(x)的图象关于直线x=x0对称,则有( )
| 1 |
| a |
A、x0≤
| ||
B、x0>
| ||
C、x0<
| ||
D、x0≥
|