Question

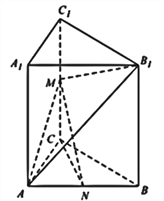
【题目】如图，在三棱柱ABC–A1B1C1中，AB＝BC，D为AC的中点，O为四边形B1C1CB的对角线的交点，AC⊥BC1．求证：

（1）OD∥平面A1ABB1；

（2）平面A1C1CA⊥平面BC1D．

Answer 1

【答案】（1）详见解析；（2）详见解析.

【解析】

（1）连结，根据三棱柱的性质，得到四边形为平行四边形，从而得到O为的中点，结合题的条件，得到，利用线面平行的判定定理证得结果；

（2）利用等腰三角形，得到，又因为，之后应用线面垂直的判定定理证得平面，再应用面面垂直的判定定理证得平面平面．

证明：（1）连结，在三棱柱中，

四边形为平行四边形，

从而O为平行四边形对角线的交点，所以O为的中点．

又D是AC的中点，从而在，中，有，

又平面，平面，

所以平面．

（2）在中，因为，D为AC的中点，

所以．

又因为，

，，平面，

所以平面，

因为平面，

所以平面平面．