题目内容
【题目】如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.
(Ⅰ)证明:平面ACD⊥平面ABC;
(Ⅱ)过AC的平面交BD于点E,若平面AEC把四面体ABCD分成体积相等的两部分,求二面角D﹣AE﹣C的余弦值.
【答案】(Ⅰ)证明:如图所示,取AC的中点O,连接BO,OD.
∵△ABC是等边三角形,∴OB⊥AC.
△ABD与△CBD中,AB=BD=BC,∠ABD=∠CBD,
∴△ABD≌△CBD,∴AD=CD.
∵△ACD是直角三角形,
∴AC是斜边,∴∠ADC=90°.
∴DO= ![]() AC.
AC.
∴DO2+BO2=AB2=BD2 .
∴∠BOD=90°.
∴OB⊥OD.
又DO∩AC=O,∴OB⊥平面ACD.
又OB平面ABC,
∴平面ACD⊥平面ABC.
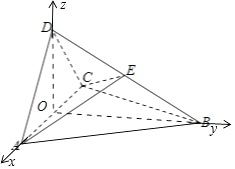
(Ⅱ)解:设点D,B到平面ACE的距离分别为hD , hE . 则 ![]() =
= ![]() .
.
∵平面AEC把四面体ABCD分成体积相等的两部分,
∴ 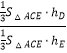 =
= ![]() =
= ![]() =1.
=1.
∴点E是BD的中点.
建立如图所示的空间直角坐标系.不妨设AB=2.
则O(0,0,0),A(1,0,0),C(﹣1,0,0),D(0,0,1),B(0, ![]() ,0),E
,0),E ![]() .
.![]() =(﹣1,0,1),
=(﹣1,0,1), ![]() =
= ![]() ,
, ![]() =(﹣2,0,0).
=(﹣2,0,0).
设平面ADE的法向量为 ![]() =(x,y,z),则
=(x,y,z),则 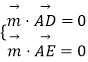 ,即
,即 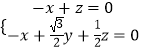 ,取
,取 ![]() =
= ![]() .
.
同理可得:平面ACE的法向量为 ![]() =(0,1,
=(0,1, ![]() ).
).
∴cos ![]() =
= ![]() =
= ![]() =﹣
=﹣ ![]() .
.
∴二面角D﹣AE﹣C的余弦值为 ![]() .
.
【解析】(Ⅰ)如图所示,取AC的中点O,连接BO,OD.△ABC是等边三角形,可得OB⊥AC.由已知可得:△ABD≌△CBD,AD=CD.△ACD是直角三角形,可得AC是斜边,∠ADC=90°.可得DO= ![]() AC.利用DO2+BO2=AB2=BD2 . 可得OB⊥OD.利用线面面面垂直的判定与性质定理即可证明.
AC.利用DO2+BO2=AB2=BD2 . 可得OB⊥OD.利用线面面面垂直的判定与性质定理即可证明.
(Ⅱ)设点D,B到平面ACE的距离分别为hD , hE . 则 ![]() =
= ![]() .根据平面AEC把四面体ABCD分成体积相等的两部分,可得
.根据平面AEC把四面体ABCD分成体积相等的两部分,可得 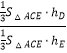 =
= ![]() =
= ![]() =1,即点E是BD的中点.建立如图所示的空间直角坐标系.设AB=2.利用法向量的夹角公式即可得出.
=1,即点E是BD的中点.建立如图所示的空间直角坐标系.设AB=2.利用法向量的夹角公式即可得出.
【考点精析】掌握平面与平面垂直的判定是解答本题的根本,需要知道一个平面过另一个平面的垂线,则这两个平面垂直.

 名校课堂系列答案
名校课堂系列答案【题目】某商场为了解该商场某商品近5年日销售量(单位:件),随机抽取近5年50天的销售量,统计结果如下:
日销售量 | 100 | 150 |
天数 | 30 | 20 |
频率 |
|
|
若将上表中频率视为概率,且每天的销售量相互独立.则在这5年中:
(1)求5天中恰好有3天销售量为150件的概率(用分式表示);
(2)已知每件该商品的利润为20元,用X表示该商品某两天销售的利润和(单位: 元),求X的分布列和数学期望.
【题目】如图,在三棱柱ABC–A1B1C1中,AB=BC,D为AC的中点,O为四边形B1C1CB的对角线的交点,AC⊥BC1.求证:

(1)OD∥平面A1ABB1;
(2)平面A1C1CA⊥平面BC1D.
【题目】共享单车已成为一种时髦的新型环保交通工具,某共享单车公司为了拓展市场,对![]() ,
,![]() 两个品牌的共享单车在编号分别为1,2,3,4,5的五个城市的用户人数(单位:十万)进行统计,得到数据如下:
两个品牌的共享单车在编号分别为1,2,3,4,5的五个城市的用户人数(单位:十万)进行统计,得到数据如下:
城市品牌 | 1 | 2 | 3 | 4 | 5 |
| 3 | 4 | 12 | 6 | 8 |
| 4 | 3 | 7 | 9 | 5 |
(Ⅰ)若共享单车用户人数超过50万的城市称为“优城”,否则称为“非优城”,据此判断能否有![]() 的把握认为“优城”和共享单车品牌有关?
的把握认为“优城”和共享单车品牌有关?
(Ⅱ)若不考虑其它因素,为了拓展市场,对![]() 品牌要从这五个城市选择三个城市进行宣传.
品牌要从这五个城市选择三个城市进行宣传.
(i)求城市2被选中的概率;
(ii)求在城市2被选中的条件下城市3也被选中的概率.
附:参考公式及数据
| 0.15 | 0.10 | 0.05 | 0.025 | 0.005 | 0.001 | |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]()
【题目】某电信公司从所在地的1000名使用4G手机用户中,随机抽取了20名,对其收集每日使用流量(单位:M)进行统计,得到如下数据:
流量x | 0≤x<5 | 5≤x<10 | 10≤x<15 | 15≤x<20 | 20≤x<25 | x≥25 |
人数 | 1 | 6 | 6 | 5 | 2 | 0 |
(1)估计这20名4G手机用户每日使用流量(单位:M)的平均值;
(2)估计此地1000名使用4G手机用户中每日使用流量不少于10M用户数;
(3)在15≤x<20和20≤x<25两组用户中,随机抽取两人作进一步问卷调查,求所抽取的两人恰好来自不同组的概率.

