题目内容
【题目】在平面直角坐标系![]() 中,已知
中,已知![]() 为三个不同的定点.以原点
为三个不同的定点.以原点![]() 为圆心的圆与线段
为圆心的圆与线段![]() 都相切.
都相切.
(Ⅰ)求圆![]() 的方程及
的方程及![]() 的值;
的值;
(Ⅱ)若直线![]() 与圆
与圆![]() 相交于
相交于![]() 两点,且
两点,且![]() ,求
,求![]() 的值;
的值;
(Ⅲ)在直线![]() 上是否存在异于
上是否存在异于![]() 的定点
的定点![]() ,使得对圆
,使得对圆![]() 上任意一点
上任意一点![]() ,都有
,都有 为常数
为常数![]() ?若存在,求出点
?若存在,求出点![]() 的坐标及
的坐标及![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(Ⅰ)![]() ,
,![]()
![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)见解析
;(Ⅲ)见解析
【解析】
(Ⅰ)根据直线与圆相切,圆心到直线的距离等于半径求解;(Ⅱ)用坐标表示向量积,再联立直线与圆方程,消元代入向量积求解;(Ⅲ)假设A、P的坐标,根据两点距离公式与![]() 建立等式,再根据A、P分别满足直线和圆的方程化简等式,最后根据等式恒成立的条件求解.
建立等式,再根据A、P分别满足直线和圆的方程化简等式,最后根据等式恒成立的条件求解.
(Ⅰ)由于圆![]() 与线段
与线段![]() 相切,所以半径
相切,所以半径![]() .
.
即圆![]() 的方程为
的方程为![]() .
.
又由题![]() 与线段
与线段![]() 相切,
相切,
所以线段![]() 方程为
方程为![]() .即
.即![]() .
.
故直线![]() 的方程为
的方程为![]() .
.
由直线![]() 和圆
和圆![]() 相切可得:
相切可得: ,
,
解得![]() 或
或![]() .由于
.由于![]() 为不同的点,所以
为不同的点,所以![]() .
.
(Ⅱ)设![]() ,
,![]() ,则
,则![]() .
.
由![]() 可得
可得![]() ,
,
![]() ,解得
,解得![]() .所以
.所以![]() .
.
故![]() .
.
所以![]() .所以
.所以![]() .
.
故![]() .
.
(Ⅲ)设![]() .
.
则![]() ,
,![]() .
.
若在直线![]() 上存在异于
上存在异于![]() 的定点
的定点![]() ,使得对圆
,使得对圆![]() 上任意一点
上任意一点![]() ,
,
都有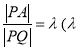 为常数
为常数![]() ,
,
等价于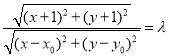 对圆
对圆![]() 上任意点
上任意点![]() 恒成立.
恒成立.
即![]() .
.
整理得![]() .
.
因为点![]() 在直线
在直线![]() 上,所以
上,所以![]() .
.
由于![]() 在圆
在圆![]() 上,所以
上,所以![]() .
.
故![]() 对任意
对任意![]() 恒成立.
恒成立.
所以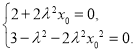 显然
显然![]() ,所以
,所以![]() .
.
故![]() ,
,
因为![]() ,解得
,解得![]() 或
或![]() .
.
当![]() 时,
时,![]() ,此时
,此时![]() 重合,舍去.
重合,舍去.
当![]() 时,
时,![]() ,
,
综上,存在满足条件的定点![]() ,此时
,此时![]() .
.

【题目】如图,在三棱柱ABC–A1B1C1中,AB=BC,D为AC的中点,O为四边形B1C1CB的对角线的交点,AC⊥BC1.求证:

(1)OD∥平面A1ABB1;
(2)平面A1C1CA⊥平面BC1D.
【题目】共享单车已成为一种时髦的新型环保交通工具,某共享单车公司为了拓展市场,对![]() ,
,![]() 两个品牌的共享单车在编号分别为1,2,3,4,5的五个城市的用户人数(单位:十万)进行统计,得到数据如下:
两个品牌的共享单车在编号分别为1,2,3,4,5的五个城市的用户人数(单位:十万)进行统计,得到数据如下:
城市品牌 | 1 | 2 | 3 | 4 | 5 |
| 3 | 4 | 12 | 6 | 8 |
| 4 | 3 | 7 | 9 | 5 |
(Ⅰ)若共享单车用户人数超过50万的城市称为“优城”,否则称为“非优城”,据此判断能否有![]() 的把握认为“优城”和共享单车品牌有关?
的把握认为“优城”和共享单车品牌有关?
(Ⅱ)若不考虑其它因素,为了拓展市场,对![]() 品牌要从这五个城市选择三个城市进行宣传.
品牌要从这五个城市选择三个城市进行宣传.
(i)求城市2被选中的概率;
(ii)求在城市2被选中的条件下城市3也被选中的概率.
附:参考公式及数据
| 0.15 | 0.10 | 0.05 | 0.025 | 0.005 | 0.001 | |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]()

