题目内容
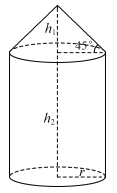
【题目】如图所示的某种容器的体积为![]() ,它是由圆锥和圆柱两部分连结而成的,圆柱与圆锥的底面圆半径都为
,它是由圆锥和圆柱两部分连结而成的,圆柱与圆锥的底面圆半径都为![]() .圆锥的高为
.圆锥的高为![]() ,母线与底面所成的角为
,母线与底面所成的角为![]() ;圆柱的高为
;圆柱的高为![]() .已知圆柱底面造价为
.已知圆柱底面造价为![]() 元
元![]() ,圆柱侧面造价为
,圆柱侧面造价为![]() 元
元![]() ,圆锥侧面造价为
,圆锥侧面造价为![]() 元
元![]() .
.
(1)将圆柱的高![]() 表示为底面圆半径
表示为底面圆半径![]() 的函数,并求出定义域;
的函数,并求出定义域;
(2)当容器造价最低时,圆柱的底面圆半径![]() 为多少?
为多少?
【答案】(1)![]() ,定义域为
,定义域为![]() .(2)
.(2)![]()
【解析】
(1)由题![]() 由圆柱与圆锥体积公式得
由圆柱与圆锥体积公式得![]() ,得
,得![]() 即可;(2)由圆柱与圆锥的侧面积公式得容器总造价为
即可;(2)由圆柱与圆锥的侧面积公式得容器总造价为![]() ,求导求最值即可
,求导求最值即可
(1)因为圆锥的母线与底面所成的角为![]() ,所以
,所以![]() ,
,
圆锥的体积为![]() ,圆柱的体积为
,圆柱的体积为![]() .
.
因为![]() ,所以
,所以![]() ,
,
所以![]() .
.
因为![]() ,所以
,所以![]() .
.
因此![]() .
.
所以![]() ,定义域为
,定义域为![]() .
.
(2)圆锥的侧面积![]() ,
,
圆柱的侧面积![]() ,底面积
,底面积![]() .
.
容器总造价为![]()
![]()
![]() .
.
令![]() ,则
,则![]() .令
.令![]() ,得
,得![]() .
.
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上为单调减函数;
上为单调减函数;
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上为单调增函数.
上为单调增函数.
因此,当且仅当![]() 时,
时,![]() 有最小值,即
有最小值,即![]() 有最小值,为
有最小值,为![]() 元.
元.
所以总造价最低时,圆柱的底面圆半径为![]() .
.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
【题目】某工厂今年前5个月某种产品的产量(单位:万件)的数据如下表:
| 1 | 2 | 3 | 4 | 5 |
| 4 | 5 | 4 | 6 | 6 |
(1)若从这5组数据中随机抽出2组,求抽出的2组数据恰好是不相邻两个月的数据的概率;
(2)求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并估计今年6月份该种产品的产量.
,并估计今年6月份该种产品的产量.
参考公式: .
.