题目内容
(本小题满分15分)
已知圆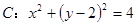 ,
,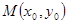 为抛物线
为抛物线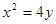 上的动点.
上的动点.
(Ⅰ) 若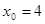 ,求过点
,求过点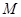 的圆的切线方程;
的圆的切线方程;
(Ⅱ) 若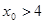 ,求过点
,求过点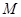 的圆的两切线与
的圆的两切线与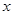 轴围成的三角形面积
轴围成的三角形面积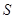 的最小值.
的最小值.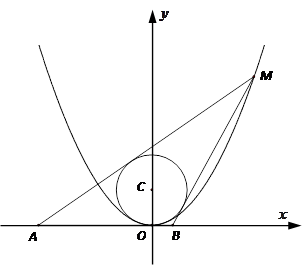
已知圆
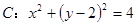 ,
,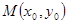 为抛物线
为抛物线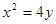 上的动点.
上的动点.(Ⅰ) 若
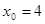 ,求过点
,求过点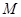 的圆的切线方程;
的圆的切线方程;(Ⅱ) 若
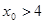 ,求过点
,求过点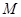 的圆的两切线与
的圆的两切线与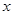 轴围成的三角形面积
轴围成的三角形面积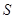 的最小值.
的最小值.
(Ⅰ)切线方程为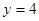 或
或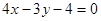 .
.
(Ⅱ)两切线与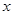 轴围成的三角形面积
轴围成的三角形面积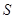 的最小值为32.
的最小值为32.
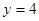 或
或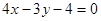 .
.(Ⅱ)两切线与
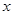 轴围成的三角形面积
轴围成的三角形面积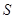 的最小值为32.
的最小值为32.本试题主要是考查了导数在研究函数中的运用,求解切线方程以及三角形面积的求解的综合运用。
(1)因为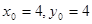 .当点
.当点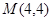 时,设切线方程为
时,设切线方程为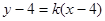 ,即
,即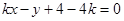 ,利用导数的几何意义得到k的值,得到结论。
,利用导数的几何意义得到k的值,得到结论。
(2)设切线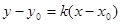 ,即
,即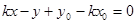 ,
,
切线与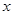 轴交点为
轴交点为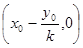 ,圆心到切线的距离为
,圆心到切线的距离为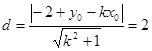 .
.
表示得到三角形的面积的公式,然后结合函数求解得到最值。
解:(Ⅰ)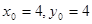 .
.
当点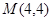 时,设切线方程为
时,设切线方程为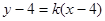 ,即
,即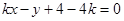 .
.
圆心到切线的距离为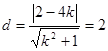 ,即
,即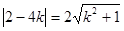 .
.
所以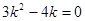 ,得
,得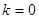 或
或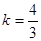 .
.
所以切线方程为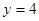 或
或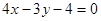 .………………………………………………6分
.………………………………………………6分
(Ⅱ)设切线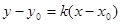 ,即
,即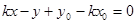 ,
,
切线与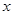 轴交点为
轴交点为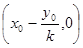 ,圆心到切线的距离为
,圆心到切线的距离为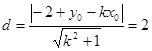 .
.
即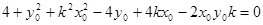 ,
,
化简得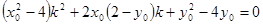
设两切线斜率分别为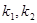 ,则
,则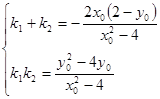 ,
,
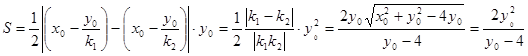
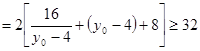 ,当且仅当
,当且仅当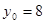 时取等号.
时取等号.
所以两切线与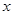 轴围成的三角形面积
轴围成的三角形面积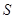 的最小值为32.………………………………15分
的最小值为32.………………………………15分
(1)因为
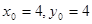 .当点
.当点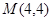 时,设切线方程为
时,设切线方程为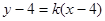 ,即
,即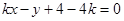 ,利用导数的几何意义得到k的值,得到结论。
,利用导数的几何意义得到k的值,得到结论。(2)设切线
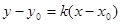 ,即
,即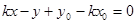 ,
,切线与
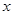 轴交点为
轴交点为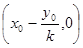 ,圆心到切线的距离为
,圆心到切线的距离为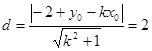 .
.表示得到三角形的面积的公式,然后结合函数求解得到最值。
解:(Ⅰ)
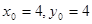 .
.当点
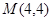 时,设切线方程为
时,设切线方程为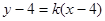 ,即
,即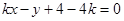 .
.圆心到切线的距离为
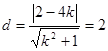 ,即
,即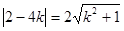 .
.所以
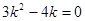 ,得
,得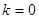 或
或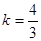 .
.所以切线方程为
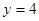 或
或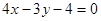 .………………………………………………6分
.………………………………………………6分(Ⅱ)设切线
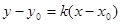 ,即
,即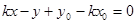 ,
,切线与
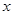 轴交点为
轴交点为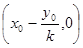 ,圆心到切线的距离为
,圆心到切线的距离为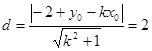 .
.即
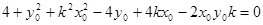 ,
,化简得
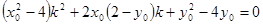
设两切线斜率分别为
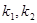 ,则
,则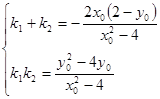 ,
,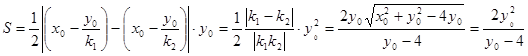
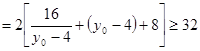 ,当且仅当
,当且仅当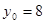 时取等号.
时取等号.所以两切线与
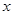 轴围成的三角形面积
轴围成的三角形面积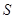 的最小值为32.………………………………15分
的最小值为32.………………………………15分
练习册系列答案
相关题目
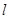 的方程为
的方程为 ,在直角坐标系
,在直角坐标系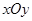 中,圆
中,圆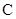 的参数方程为
的参数方程为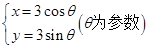 .
.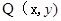 是曲线
是曲线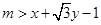 有解,求
有解,求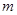 的取值范围.
的取值范围.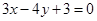 与圆
与圆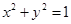 相交所截的弦长为( )
相交所截的弦长为( )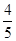
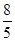
 内一点
内一点 ,过点
,过点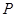 的直线
的直线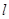 的倾斜角为
的倾斜角为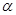 ,直线
,直线 两点.
两点.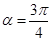 时,求弦
时,求弦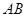 的长;
的长;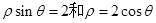 上的动点,则|MN|的最小值是 .
上的动点,则|MN|的最小值是 .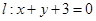 和圆
和圆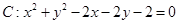 ,设A是直线
,设A是直线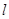 上动点,直线AC交圆于点B,若在圆C上存在点M,使
上动点,直线AC交圆于点B,若在圆C上存在点M,使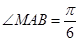 ,则点A的横坐标的取值范围为 。
,则点A的横坐标的取值范围为 。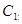
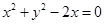 与圆
与圆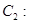
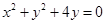 的位置关系为 .
的位置关系为 .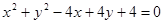 上有四点到直线
上有四点到直线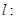
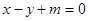 的距离为
的距离为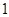 ,则
,则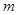 的取值范围为______________.
的取值范围为______________.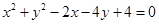 相交所得弦的长为2,则该直线的方程为________;
相交所得弦的长为2,则该直线的方程为________;