题目内容
已知方程
+
=1表示椭圆,则m的取值范围是 .
| x2 |
| 2m2-1 |
| y2 |
| m |
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:要使原方程表示椭圆,则m便满足
,解该不等式组即得m的取值范围.
|
解答:
解:由已知条件知,m满足:
,解得:m>
,且m≠1;
∴m的取值范围是{m|m>
,且m≠1}.
故答案为:{m|m>
,且m≠1}.
|
| ||
| 2 |
∴m的取值范围是{m|m>
| ||
| 2 |
故答案为:{m|m>
| ||
| 2 |
点评:考查椭圆的标准方程,以及解一元二次不等式.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
如果奇函数f(x)在[3,6]上是增函数且最大值是4,那么f(x)在[-6,-3]上是( )
| A、减函数且最小值是-4 |
| B、减函数且最大值是-4 |
| C、增函数且最小值是-4 |
| D、增函数且最大值是-4 |
集合M={y|y=x2-1},N={y|y=3-x2},则M∩N等于( )
| A、{y|-1≤y≤3} |
| B、{(-1,2),(1,2)} |
| C、∅ |
| D、R |
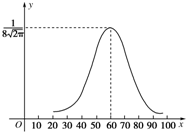 某校1000名学生的某次数学考试成绩X服从正态分布,其密度函数曲线如图,则成绩X位于区间(53,68]的人数大约是
某校1000名学生的某次数学考试成绩X服从正态分布,其密度函数曲线如图,则成绩X位于区间(53,68]的人数大约是