题目内容
设函数f(x)=x3-12x+5,x∈R.
(1)求函数f(x)的单调区间和极值;
(2)若关于x的方程f(x)=a有三个不同实根,求实数a的取值范围;
(1)求函数f(x)的单调区间和极值;
(2)若关于x的方程f(x)=a有三个不同实根,求实数a的取值范围;
(1)f(x)的单调递增区间为(-∞,-2)和(2,+∞);单调减区间为(-2,2)当x=-2时,f(x)有极大值21;当x=2时,f(x)有极小值-11.
(2)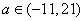
(2)
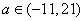
试题分析:解:(1)f′(x)=3x2-12,令f′(x)=0,解得x1=-2,x2=2. 2分
因为当x>2或x<-2时,f′(x)>0;当-2<x<2时,f′(x)<0.
所以f(x)的单调递增区间为(-∞,-2)和(2,+∞);单调减区间为(-2,2). 3分
当x=-2时,f(x)有极大值21;当x=2时,f(x)有极小值-11. 2分
(2)由(1)的分析知y=f(x)的图象的大致形状及走向,当-11<a<21时,直线y=a与y=f(x)的
图象有三个不同交点,即方程f(x)=a有三个不同的解.
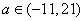 2分
2分点评:主要是考查了导数在研究函数中单调性和极值的运用,属于基础题。

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
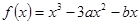 ,其中
,其中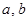 为实数.
为实数.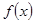 在
在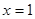 处取得的极值为
处取得的极值为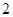 ,求
,求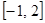 上为减函数,且
上为减函数,且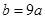 ,求
,求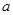 的取值范围.
的取值范围.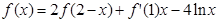 ,则
,则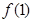 等于( )
等于( )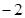
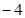
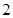
 是曲线
是曲线 上任意一点, 则点
上任意一点, 则点 的距离的最小值是( )
的距离的最小值是( )

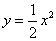 与直线
与直线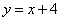 所围成的图形的面积是
所围成的图形的面积是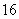
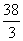
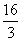
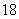
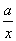 .
.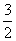 ,求a的值;
,求a的值;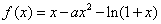 ,其中
,其中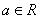 .
.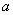 =1时,求
=1时,求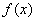 在(1,
在(1,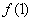 )的切线方程
)的切线方程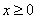 时,
时,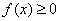 ,求实数
,求实数 ,若函数
,若函数 有大于零的极值点,则
有大于零的极值点,则 的取值范围是
的取值范围是  若满足(x-1)
若满足(x-1) >0,则必有( )
>0,则必有( )