题目内容
用数学归纳法证明:
详见解析
解析试题分析:由数学归纳法证明不等式的一般步骤可知:第一步应验证初值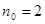 时不等式成立;第二步进行归纳假设:假设当
时不等式成立;第二步进行归纳假设:假设当 时所证不等式成立,在此基础上来证明当
时所证不等式成立,在此基础上来证明当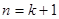 时所证不等式也成立;特别注意在证
时所证不等式也成立;特别注意在证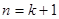 时一定要用到
时一定要用到 时的结论;第三步下结论:在第一步及第二步的基础上就可得出所证不等式对一切
时的结论;第三步下结论:在第一步及第二步的基础上就可得出所证不等式对一切 都成立.
都成立.
试题解析:证明:(1)当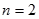 时,
时,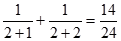 ,
, 命题成立。
命题成立。
(2)假设当 时,
时,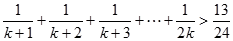 成立
成立
当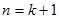 时,
时,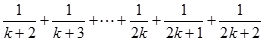

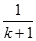 +
+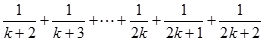
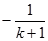
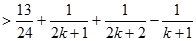
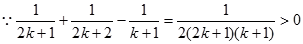

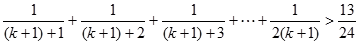
当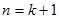 时命题成立。
时命题成立。
所以对于任意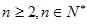 都成立.
都成立.
考点:数学归纳法.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
 的圆的内接矩形中,以正方形的面积为最大,最大值为
的圆的内接矩形中,以正方形的面积为最大,最大值为 .”猜想关于球的相应命题为“半径为
.”猜想关于球的相应命题为“半径为




 个等式,并猜测第
个等式,并猜测第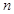 (
(
 )个等式;
)个等式; ,试证明
,试证明 至少有一个不小于1.
至少有一个不小于1. ,整数
,整数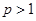 ,
, .
. 且
且 时,
时, ;
; 满足
满足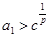 ,
,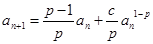 ,证明:
,证明: .
. .
. 的三边长分别为
的三边长分别为 内切圆半径为
内切圆半径为 ,则三角形面积
,则三角形面积 ” .拓展到空间,类比上述结论,“若四面体
” .拓展到空间,类比上述结论,“若四面体 的四个面的面积分别为
的四个面的面积分别为 内切球的半径为
内切球的半径为 ,由不等式
,由不等式 启发我们可以得到推广结论:
启发我们可以得到推广结论: ,则
,则
 的前
的前 项和为
项和为 ,则
,则 ,
, ,
, ,
, 成等差数列.类比
成等差数列.类比 的前
的前 ,则
,则 , ,
, , 成等比数列.
成等比数列.