题目内容
在平面几何里，有：“若
的三边长分别为
内切圆半径为
，则三角形面积
” ．拓展到空间，类比上述结论，“若四面体
的四个面的面积分别为
内切球的半径为，则四面体的体积为 ”．
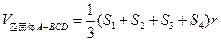
解析
练习册系列答案
阅读快车系列答案
相关题目
阅读快车系列答案题目内容
在平面几何里，有：“若的三边长分别为内切圆半径为，则三角形面积” ．拓展到空间，类比上述结论，“若四面体的四个面的面积分别为内切球的半径为，则四面体的体积为 ”．
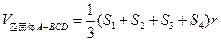
解析
阅读快车系列答案
，
观察
……
，
，
三种，其中
是正整数
的最佳分解时，我们规定函数
，例如
.关于函数
有下列叙述：①
，②
，③
，④
.其中正确的序号为 （填入所有正确的序号）．
，其中任意两条直线都不平行，任意三条直线都不过同一点。若
用
表示这n条直线交点的个数，则
为等差数列，则当
时，数列
也是等差数列；类比上述性质，相应地，若数列
是正项等比数列，当
_ 时，
也是等比数列．
中，两直角边分别为
，斜边上的高为
，则
。由此类比，在
三棱锥
中的三条棱
两两垂直且长度分别为
。设棱锥底面
上的高为
根据上述规律，第五个等式为______________________________________
时
（用含
的式子表示）