题目内容
13．已知△ABC的三条边长分别为3，4，5，如果把三角形的三边都增加相同的长度，则这个新三角形的形状为（ ）| A． | 锐角三角形 | B． | 直角三角形 | ||
| C． | 钝角三角形 | D． | 由增加的长度决定 |
分析 设三边分别为：3+x，4+x，5+x，由余弦定理可得最大角的余弦值，可判最大角为锐角，可得结论．
解答 解：设每条边长增加相同的长度x，（x＞0）
则三边分别为：3+x，4+x，5+x，
设最长边5+x对的角为α，
由余弦定理可得cosα=$\frac{（3+x）^{2}+（4+x）^{2}-（5+x）^{2}}{2（3+x）（4+x）}$
=$\frac{x}{2（3+x）}$＞0，∴最大角为锐角，
∴新三角形为锐角三角形，
故选：A．
点评 本题考查三角形形状的判断，涉及余弦定理的应用是，属基础题．
练习册系列答案
怎样学好牛津英语系列答案
相关题目
5．已知sinθcosθ＜0，那么角θ是（ ）
| A． | 第一或第二象限角 | B． | 第二或第三象限角 | ||
| C． | 第二或第四象限角 | D． | 第一或第四象限角 |
5．如图，在△ABC中，AD⊥AB，$\overrightarrow{BC}$=$\sqrt{3}$$\overrightarrow{BD}$，|$\overrightarrow{AD}$|=1，则$\overrightarrow{AD}$•$\overrightarrow{AC}$的值为（ ）
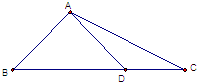
| A． | $\sqrt{3}$ | B． | 3 | C． | $\frac{\sqrt{2}}{2}$ | D． | $\sqrt{5}$ |
，若方程
有四个不同的解
，且
，则
的取值范围是（ ）
B．
C．
D．
18．据媒体报道：某市4月份空气质量优良，高居全国榜首，青春中学九年级课外兴趣小组据此提出了“今年究竟能有多少天空气质量达到优良”的问题，他们根据国家环保总局所公布的空气质量级别表（见表1）以及市环保监测站提供的资料，从中随机抽取了今年1～4月份中30天空气综合污染指数，统计数据如下：
表1：空气质量级别表
空气综合污染指数
30，32，40，42，45，45，77，83，85，87，90，113，127，153，167，
38，45，48，53，57，64，66，77，92，98，130，184，201，235，243．
请根据空气质量级别表和抽查的空气综合污染指数，解答以下问题：
（1）填写频率分布表中未完成的空格；
（2）写出统计数据中的中位数、众数；
（3）请根据抽样数据，估计该市今年（按360天计算）空气质量是优良（包括Ⅰ、Ⅱ级）的天数．
表1：空气质量级别表
| 空气污染指数 | 0～50 | 51～100 | 101～150 | 151～200 | 201～250 | 251～300 | 大于300 |
| 空气质量级别 | Ⅰ级（优） | Ⅱ级（良） | Ⅲ1（轻微污染） | Ⅲ2（轻度污染） | Ⅳ1（中度污染） | Ⅳ2（中度重污染） | Ⅴ（重度污染） |
30，32，40，42，45，45，77，83，85，87，90，113，127，153，167，
38，45，48，53，57，64，66，77，92，98，130，184，201，235，243．
请根据空气质量级别表和抽查的空气综合污染指数，解答以下问题：
（1）填写频率分布表中未完成的空格；
| 分组 | 频数统计 | 频数 | 频率 |
| 0～50 | 0.30 | ||
| 51～100 |  | 12 | 0.40 |
| 101～150 | |||
| 151～200 |  | 3 | 0.10 |
| 201～250 | | 3 | 0.10 |
| 合计 | 30 | 30 | 1.00 |
（3）请根据抽样数据，估计该市今年（按360天计算）空气质量是优良（包括Ⅰ、Ⅱ级）的天数．
的图象如右图所示，则下列函数图象正确的是（ ）
B．
D．
和两条不重合的直线
，则下列四个命题中不正确的是（ ）
，则
，则
，则
，则