题目内容
10.已知随机变量X服从正态分布N(1,σ2),且P(-2≤X≤1)=0.4,则P(X>4)=( )| A. | 0.1 | B. | 0.2 | C. | 0.3 | D. | 0.6 |
分析 随机变量ξ服从正态分布N(1,σ2),得到曲线关于x=1对称,根据曲线的对称性得到结果.
解答 解:随机变量ξ服从正态分布N(1,σ2),
∴曲线关于x=1对称,
∴P(X>4)=P(X<-2)=1-P(-2≤X≤1)=0.1
故选:A.
点评 本题主要考查正态分布曲线的特点及曲线所表示的意义、函数图象对称性的应用等基础知识,属于基础题.

练习册系列答案
相关题目
18.如果向量$\overrightarrow{a}$=(1,0),$\overrightarrow{b}$=(-2,4),那么|$\overrightarrow{a}$+3$\overrightarrow{b}$|的值是( )
| A. | 13 | B. | 12 | C. | 5 | D. | 4 |
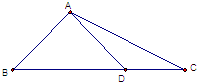
5.如图,在△ABC中,AD⊥AB,$\overrightarrow{BC}$=$\sqrt{3}$$\overrightarrow{BD}$,|$\overrightarrow{AD}$|=1,则$\overrightarrow{AD}$•$\overrightarrow{AC}$的值为( )

| A. | $\sqrt{3}$ | B. | 3 | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{5}$ |
15.在数列{an}中,已知对于n∈N*,有a1+a2+a3+…+an=2n-1,则a${\;}_{1}^{2}$+a${\;}_{2}^{2}$+…+a${\;}_{n}^{2}$=( )
| A. | 4n-1 | B. | $\frac{1}{3}$(4n-1) | C. | $\frac{1}{3}$(2n-1) | D. | (2n-1)2 |
18.据媒体报道:某市4月份空气质量优良,高居全国榜首,青春中学九年级课外兴趣小组据此提出了“今年究竟能有多少天空气质量达到优良”的问题,他们根据国家环保总局所公布的空气质量级别表(见表1)以及市环保监测站提供的资料,从中随机抽取了今年1~4月份中30天空气综合污染指数,统计数据如下:
表1:空气质量级别表
空气综合污染指数
30,32,40,42,45,45,77,83,85,87,90,113,127,153,167,
38,45,48,53,57,64,66,77,92,98,130,184,201,235,243.
请根据空气质量级别表和抽查的空气综合污染指数,解答以下问题:
(1)填写频率分布表中未完成的空格;
(2)写出统计数据中的中位数、众数;
(3)请根据抽样数据,估计该市今年(按360天计算)空气质量是优良(包括Ⅰ、Ⅱ级)的天数.
表1:空气质量级别表
| 空气污染指数 | 0~50 | 51~100 | 101~150 | 151~200 | 201~250 | 251~300 | 大于300 |
| 空气质量级别 | Ⅰ级(优) | Ⅱ级(良) | Ⅲ1(轻微污染) | Ⅲ2(轻度污染) | Ⅳ1(中度污染) | Ⅳ2(中度重污染) | Ⅴ(重度污染) |
30,32,40,42,45,45,77,83,85,87,90,113,127,153,167,
38,45,48,53,57,64,66,77,92,98,130,184,201,235,243.
请根据空气质量级别表和抽查的空气综合污染指数,解答以下问题:
(1)填写频率分布表中未完成的空格;
| 分组 | 频数统计 | 频数 | 频率 |
| 0~50 | 0.30 | ||
| 51~100 |  | 12 | 0.40 |
| 101~150 | |||
| 151~200 |  | 3 | 0.10 |
| 201~250 |  | 3 | 0.10 |
| 合计 | 30 | 30 | 1.00 |
(3)请根据抽样数据,估计该市今年(按360天计算)空气质量是优良(包括Ⅰ、Ⅱ级)的天数.
 中,
中, ,
, ,
, ,则
,则 的值为 .
的值为 .