题目内容
【题目】过双曲线C:![]() =1的右焦点F且与x轴不重合的直线交双曲线C于A、B两个点,定点D(
=1的右焦点F且与x轴不重合的直线交双曲线C于A、B两个点,定点D(![]() ,0).
,0).

(1)当直线AB垂直于x轴时,求直线AD的方程.
(2)设直线AD与直线x=1相交于点E,求证:FD∥BE.
【答案】(1)![]() 或2
或2![]() x+y﹣3
x+y﹣3![]() =0;(2)见解析
=0;(2)见解析
【解析】
(1)直线AB垂直于x轴时,易求方程,同时解得点的坐标可得直线AD的方程;
(2)表示出直线AD的方程,结合与直线x=1的交点可得点E的坐标,从而可证.
(1)F(2,0)当直线AB垂直于x轴时,直线AB的方程为:x=2,可得A(2,![]() )或A(2,﹣
)或A(2,﹣![]() ),∴直线AD的方程为
),∴直线AD的方程为![]() 或2
或2![]() x+y﹣3
x+y﹣3![]() =0
=0
(2)设直线AB的方程为x=ty+2代入x2﹣y2=2得(t2﹣1)y2+4ty+2=0,
设A(x1,y1),B(x2,y2),则y1+y2=![]() ,
,
直线AD的方程为: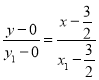 ,
,
令x=1得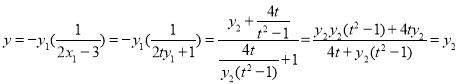
∴FD∥BE.

练习册系列答案
相关题目




