题目内容
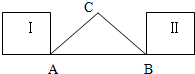
如图,在△ABC中,∠C=90°,AC=BC=2
,一个边长为2的正方形由位置Ⅰ沿AB平行移动到位置Ⅱ停止,若移动的距离为x,正方形和△ABC的公共部分的面积为f(x),试求出f(x)的解析式,并求出最大值.
| 2 |

当x∈[0,2]时,正方形和△ABC的公共部分是等腰直角三角形
∴f(x)=
x2
当x∈(2,4]时,正方形和△ABC的公共部分是两个直角梯形
f(x)=4-
(x-2)2-
(4-x)2
当x∈(4,6]时,正方形和△ABC的公共部分是等腰直角三角形
f(x)=
[2-(x-4)]2
综上所述:f(x)=
分析可得当x=3时,f(x)的最大值为3.
∴f(x)=
| 1 |
| 2 |
当x∈(2,4]时,正方形和△ABC的公共部分是两个直角梯形
f(x)=4-
| 1 |
| 2 |
| 1 |
| 2 |
当x∈(4,6]时,正方形和△ABC的公共部分是等腰直角三角形
f(x)=
| 1 |
| 2 |
综上所述:f(x)=
|
|
分析可得当x=3时,f(x)的最大值为3.

练习册系列答案
相关题目
 函数,其中
函数,其中 ,其中
,其中 。
。 的零点;
的零点; 在区间
在区间 上的单调性;
上的单调性; 上,
上,
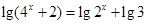 的解集为 .
的解集为 .