题目内容
(本小题满分14分)
已知 函数,其中
函数,其中 ,其中
,其中 。
。
(I)求函数 的零点;
的零点;
(II)讨论 在区间
在区间 上的单调性;
上的单调性;
(III)在区间 上,
上, 是否存在最小值?若存在,求出最小值;若不存在,请说明理由。
是否存在最小值?若存在,求出最小值;若不存在,请说明理由。
已知
 函数,其中
函数,其中 ,其中
,其中 。
。(I)求函数
 的零点;
的零点;(II)讨论
 在区间
在区间 上的单调性;
上的单调性;(III)在区间
 上,
上, 是否存在最小值?若存在,求出最小值;若不存在,请说明理由。
是否存在最小值?若存在,求出最小值;若不存在,请说明理由。(I)-a.
(II)在区间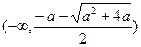 上
上 是增函数,
是增函数,
在区间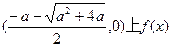 是减函数。
是减函数。
(III)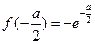
(II)在区间
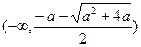 上
上 是增函数,
是增函数,在区间
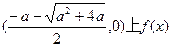 是减函数。
是减函数。(III)
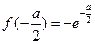
(I)解 ,得
,得 所以函数
所以函数 的零点为-a.………………2分
的零点为-a.………………2分
(II)函数 在区域(-∞,0)上有意义,
在区域(-∞,0)上有意义,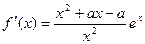 ,…………5分
,…………5分
令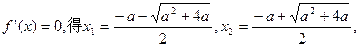
因为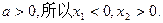 …………7分
…………7分
当x在定义域上变化时,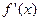 的变化情况如下:
的变化情况如下:
所以在区间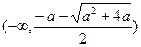 上
上 是增函数, …………8分
是增函数, …………8分
在区间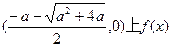 是减函数。 …………9分
是减函数。 …………9分
(III)在区间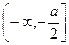 上
上 存在最小值
存在最小值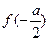 …………10分
…………10分
证明:由(I)知-a是函数 的零点,
的零点,
因为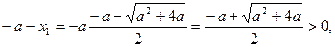
所以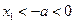 。 …………11分
。 …………11分
由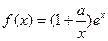 知,当
知,当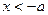 时,
时,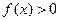 。 …………12分
。 …………12分
又函数在 上是减函数,
上是减函数,
且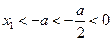 。
。
所以函数在区间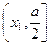 上的最小值为
上的最小值为
且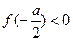 。 …………13分
。 …………13分
所以函数在区间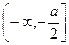 上的最小值为
上的最小值为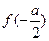 ,
,
计算得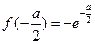 。 …………14分
。 …………14分
 ,得
,得 所以函数
所以函数 的零点为-a.………………2分
的零点为-a.………………2分(II)函数
 在区域(-∞,0)上有意义,
在区域(-∞,0)上有意义,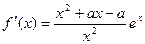 ,…………5分
,…………5分令
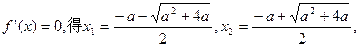
因为
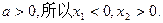 …………7分
…………7分当x在定义域上变化时,
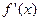 的变化情况如下:
的变化情况如下: | (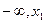 ) ) |  |
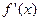 | + | - |
 |  |  |
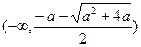 上
上 是增函数, …………8分
是增函数, …………8分在区间
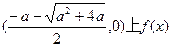 是减函数。 …………9分
是减函数。 …………9分(III)在区间
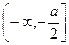 上
上 存在最小值
存在最小值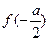 …………10分
…………10分证明:由(I)知-a是函数
 的零点,
的零点,因为
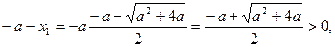
所以
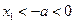 。 …………11分
。 …………11分由
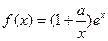 知,当
知,当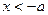 时,
时,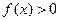 。 …………12分
。 …………12分又函数在
 上是减函数,
上是减函数,且
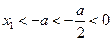 。
。所以函数在区间
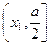 上的最小值为
上的最小值为
且
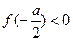 。 …………13分
。 …………13分所以函数在区间
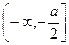 上的最小值为
上的最小值为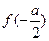 ,
,计算得
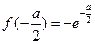 。 …………14分
。 …………14分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,
, 实系数一元二次方程
实系数一元二次方程
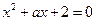 的两根都是虚数;
的两根都是虚数;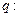 存在复数
存在复数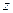 同时满足
同时满足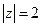 且
且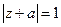 .
.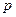 和命题
和命题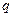 之间是否存在推出关系?请说明你的理由.
之间是否存在推出关系?请说明你的理由.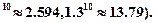
 ,其计算公式为
,其计算公式为 ,其中,
,其中, 是被测地震的最大振幅,
是被测地震的最大振幅, 是“标准地震”的振幅(使用标准地震振幅是为了修正测震仪距实际震中的距离造成的偏差).
是“标准地震”的振幅(使用标准地震振幅是为了修正测震仪距实际震中的距离造成的偏差). ,计算这次地震的震级(精确到
,计算这次地震的震级(精确到 );
); 级地震的最大振幅是5级地震
级地震的最大振幅是5级地震
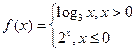 ,则
,则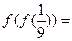 ;
; 上的根的个数 ( )
上的根的个数 ( )  )
)





 )
)





 给表
给表





 元
元 元
元