题目内容
如图,平面中两条直线l1和l2相交于点O,对于平面上任意一点M,若p、q分别是M到直线l1和l2的距离,则称有序非负实数对(p、q)是点M的“距离坐标”.已知常数p≥0,q≥0,给出下列三个命题;
①若p=q=0,则“距离坐标”为(0,0)的点有且仅有1个.
②若pq=0,且p+q≠0,则“距离坐标”为(p、q)的点有且仅有2个.
③若pq≠0,则“距离坐标”为(p、q)的点有且仅有4个.上述命题中,正确命题是 (填写序号)
①②③
解析试题分析::①p=q=0,则“距离坐标”为(0,0)的点有且只有1个,此点为点O.故①正确;②正确,p,q中有且仅有一个为0,当p为0时,坐标点在l1上,分别为关于O点对称的两点,反则在l2上也有两点,但是这两种情况不能同时存在;③正确,四个交点为与直线l1相距为p的两条平行线和与直线l2相距为q的两条平行线的交点;故答案为①②③.
考点:本题考查了距离的意义及真假命题的判断
点评:解决此类问题不仅用到分类讨论的思想方法,还要有创新意识,解题时需要注意

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
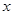 是实数,则“
是实数,则“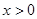 ”是“
”是“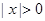 ”的____ ____条件(填充要,必要不充分,充分不必要或既不充分也不必要).
”的____ ____条件(填充要,必要不充分,充分不必要或既不充分也不必要).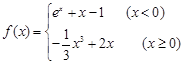 ,给出如下四个命题:
,给出如下四个命题: 在
在 上是减函数;②
上是减函数;② 有两个零点;④
有两个零点;④ 在R上恒成立.
在R上恒成立. ”的否定
”的否定 是 .
是 .  ,给出下列命题:
,给出下列命题: 有最小值;
有最小值; 时,
时, ;
; 时,
时, 上有单调性;
上有单调性; .
. ,如果存在函数
,如果存在函数 (A、B为常数),使得
(A、B为常数),使得 对一切实数
对一切实数 都成立,那么称
都成立,那么称 为函数
为函数 为函数
为函数 的一个承托函数;
的一个承托函数; 为函数
为函数 的一个承托函数。
的一个承托函数。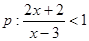 ,
,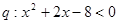 ,则
,则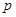 是
是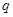 的 条件。(填“充分不必要”、“必要不充分”、“既不充分也不必要”或“充要”)
的 条件。(填“充分不必要”、“必要不充分”、“既不充分也不必要”或“充要”) 的解集为
的解集为 ,则
,则 ;
; ,若
,若 ,则
,则 或
或 的否命题是假命题;
的否命题是假命题; 中,
中, 的充要条件是
的充要条件是 ;
; 两两成的夹角均相等,则夹角的大小为
两两成的夹角均相等,则夹角的大小为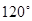 ;
;

 使函数
使函数 有意义,若
有意义,若 为假命题,则
为假命题,则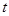 的取值范围为 .
的取值范围为 .