题目内容
【题目】已知![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,将
的中点,将![]() 沿
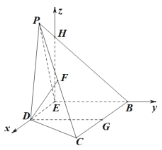
沿![]() 翻折,得到如图所示的四棱锥
翻折,得到如图所示的四棱锥![]() ,且
,且![]() ,设
,设![]() 为
为![]() 的中点.
的中点.
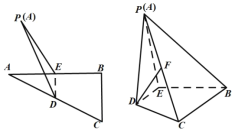
(1)证明:![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的的正弦值.
所成角的的正弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,得到四边形
,得到四边形![]() 是平行四边形,得出
是平行四边形,得出![]() ,
,![]() ,从而
,从而![]() ,
,![]() ,证得
,证得![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,进而利用线面垂直的判定定理,证得
,进而利用线面垂直的判定定理,证得![]() 平面
平面![]() ,即可得到
,即可得到![]() .
.
(2)以![]() 为坐标原点,
为坐标原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,建立如图所示的空间直角坐标系
轴,建立如图所示的空间直角坐标系![]() ,求得向量
,求得向量![]() 和平面
和平面![]() 的一个法向量,利用向量的夹角公式,即可求解.
的一个法向量,利用向量的夹角公式,即可求解.
(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,可得
,可得![]() ,且
,且![]() ,
,
所以四边形![]() 是平行四边形,所以
是平行四边形,所以![]() ,
,
因为![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,所以
的中点,所以![]() ,
,
因为![]() ,所以
,所以![]() ,
,![]() ,
,
又因为![]() ,且
,且![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,所以
,所以![]() ,
,
因为![]() 分别为
分别为![]() 的中点,故
的中点,故![]() ,
,
所以![]() ,又
,又![]() ,
,![]() ,所以
,所以![]() .
.
又因为![]() ,又
,又![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
又由![]() 平面
平面![]() ,所以
,所以![]() .
.
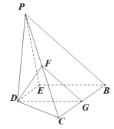
(2)由(1)知:![]() 平面
平面![]() ,以
,以![]() 为坐标原点,
为坐标原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,建立如图所示的空间直角坐标系
轴,建立如图所示的空间直角坐标系![]() ,
,
因为![]() ,可得
,可得![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
可得![]() ,所以
,所以![]() ,
,![]() ,
,
所以点![]() 到
到![]() 轴的距离为1,
轴的距离为1,
可得![]() ,
,![]() ,
,![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
所以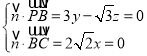 ,解得
,解得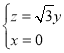 ,令
,令![]() ,可得
,可得![]() ,
,
设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() .
.
则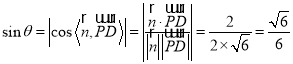 ,
,
即直线![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() .
.

 走进文言文系列答案
走进文言文系列答案【题目】已知某快递公司收取快递费的标准是:重量不超过![]() 的包裹收费
的包裹收费![]() 元;重量超过
元;重量超过![]() 的包裹,在收费
的包裹,在收费![]() 元的基础上,每超过
元的基础上,每超过![]() (不足
(不足![]() ,按
,按![]() 计算)需再收
计算)需再收![]() 元.该快递公司承揽了一个工艺品厂家的全部玻璃工艺品包裹的邮寄事宜,该厂家随机统计了
元.该快递公司承揽了一个工艺品厂家的全部玻璃工艺品包裹的邮寄事宜,该厂家随机统计了![]() 件这种包裹的两个统计数表如下:
件这种包裹的两个统计数表如下:
表![]()
包裹重量 |
|
|
|
|
|
包裹数 |
|
|
|
|
|
损坏件数 |
|
|
|
|
|
表![]()
包裹重量 |
|
|
|
|
|
出厂价(元 |
|
|
|
|
|
卖价(元 |
|
|
|
|
|
![]() 估计该快递公司对每件包裹收取快递费的平均值;
估计该快递公司对每件包裹收取快递费的平均值;
![]() 将包裹重量落入各组的频率视为概率,该工艺品厂家承担全部运费,每个包裹只有一件产品,如果客户收到有损坏品的包裹,该快递公司每件按其出厂价的
将包裹重量落入各组的频率视为概率,该工艺品厂家承担全部运费,每个包裹只有一件产品,如果客户收到有损坏品的包裹,该快递公司每件按其出厂价的![]() 赔偿给厂家.现该厂准备给客户邮寄重量在区间
赔偿给厂家.现该厂准备给客户邮寄重量在区间![]() 和
和![]() 内的工艺品各
内的工艺品各![]() 件,求该厂家这两件工艺品获得利润的分布列和期望.
件,求该厂家这两件工艺品获得利润的分布列和期望.