题目内容
(10分)已知数列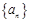 中,
中,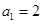 ,
,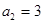 ,其前
,其前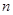 项和
项和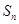
满足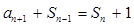
 .
.
(Ⅰ)求证:数列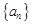 为等差数列,并求
为等差数列,并求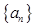 的通项公式;
的通项公式;
(Ⅱ)设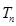 为数列
为数列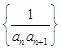 的前
的前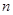 项和,求
项和,求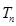
(Ⅲ)若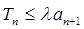 对一切
对一切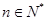 恒成立,求实数
恒成立,求实数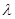 的最小值.
的最小值.
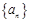 中,
中,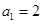 ,
,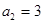 ,其前
,其前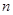 项和
项和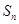
满足
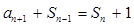
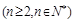 .
.(Ⅰ)求证:数列
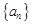 为等差数列,并求
为等差数列,并求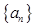 的通项公式;
的通项公式;(Ⅱ)设
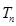 为数列
为数列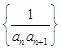 的前
的前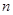 项和,求
项和,求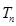
(Ⅲ)若
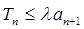 对一切
对一切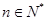 恒成立,求实数
恒成立,求实数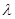 的最小值.
的最小值.解:(Ⅰ) 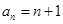 ;
;
(Ⅱ) ;
;
(Ⅲ)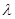 的最小值为
的最小值为
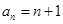 ;
;(Ⅱ)
 ;
;(Ⅲ)
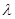 的最小值为
的最小值为
本试题主要是考查了数列的通项公式的求解和前n项和的求解,以及不等式的恒成立问题的运用。
(1)由已知, (
(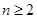 ,
,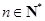 ),且
),且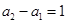
数列 是以
是以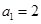 为首项,公差为1的等差数列.∴
为首项,公差为1的等差数列.∴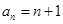
(2)因为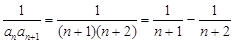
利用裂项求和得到前n项和的结论。
(3)
 ,∴
,∴ ≤
≤
∴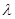 ≥
≥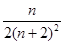
运用分离参数的思想求解其范围。
解:(Ⅰ)由已知, (
(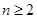 ,
,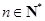 ),且
),且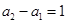
数列 是以
是以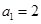 为首项,公差为1的等差数列.∴
为首项,公差为1的等差数列.∴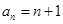 …………3分
…………3分
(Ⅱ)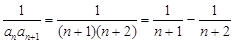
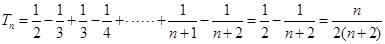 …………6分
…………6分
(Ⅲ)
 ,∴
,∴ ≤
≤
∴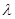 ≥
≥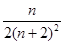
又 ≤
≤ ,(也可以利用函数的单调性解答)
,(也可以利用函数的单调性解答)
∴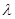 的最小值为
的最小值为 …………………………………10分
…………………………………10分
(1)由已知,
 (
(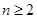 ,
,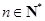 ),且
),且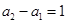
数列
 是以
是以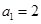 为首项,公差为1的等差数列.∴
为首项,公差为1的等差数列.∴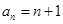
(2)因为
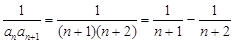
利用裂项求和得到前n项和的结论。
(3)

 ,∴
,∴ ≤
≤
∴
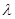 ≥
≥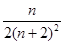
运用分离参数的思想求解其范围。
解:(Ⅰ)由已知,
 (
(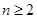 ,
,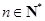 ),且
),且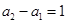
数列
 是以
是以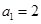 为首项,公差为1的等差数列.∴
为首项,公差为1的等差数列.∴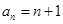 …………3分
…………3分(Ⅱ)
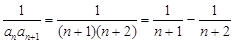
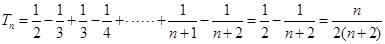 …………6分
…………6分(Ⅲ)

 ,∴
,∴ ≤
≤
∴
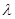 ≥
≥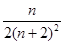
又
 ≤
≤ ,(也可以利用函数的单调性解答)
,(也可以利用函数的单调性解答)∴
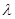 的最小值为
的最小值为 …………………………………10分
…………………………………10分
练习册系列答案
相关题目
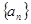 的前
的前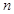 项和为
项和为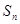 ,等比数列
,等比数列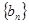 的前
的前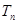 ,已知
,已知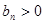
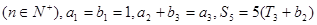 .
.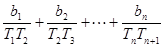 .
.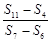 的值为 .
的值为 .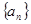 中,
中,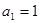 ,
,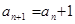 ,则
,则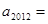
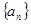 的前
的前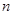 项和
项和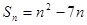 ,且满足
,且满足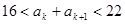 ,则正整数
,则正整数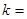 _____
_____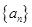 ,
,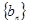 满足:
满足: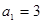 ,当
,当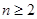 时,
时,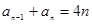 ;对于任意的正整数
;对于任意的正整数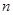 ,
,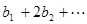
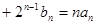 .设数列
.设数列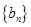 的前
的前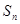 .
.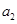 、
、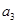 ,并求数列
,并求数列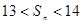 的正整数
的正整数 的通项公式为
的通项公式为 , 则它的公差为 ( )
, 则它的公差为 ( )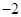
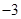
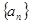 的前
的前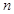 项和为
项和为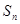 ,已知
,已知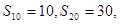 ,则
,则
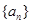 中,
中,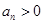 ,且
,且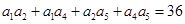 ,则
,则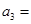 .
.